Confining/Periodic boundary conditions implementation for 2D Random Walker

Question

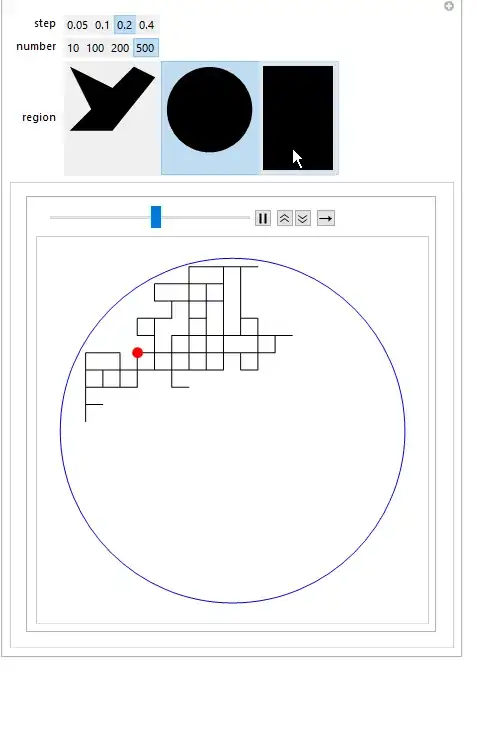
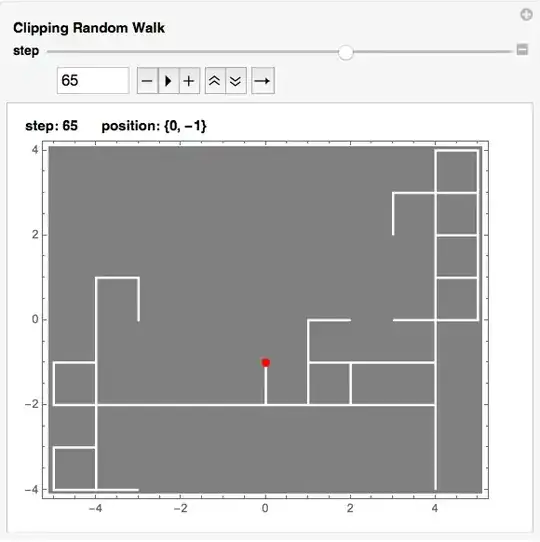
I am new to Mathematica, and am having trouble implementing confining boundary conditions for a random walk simulation confining the walker to a pre-defined region (periodic boundary conditions would be interesting as well). Right now the walker does not cross the boundary and instead makes an alternative step. I am not sure how to add an extra case where, should a step be directed outside the boundary (say the right wall) the walker would have four choices up, down, left or just remain at its current position (skip a step).

Clear[randomWalk]
randomWalk[steps_Integer, start_, region_] /; start ∈ region :=
  DynamicModule[
       {stepTypes, stepList, alternativeStep, stepChoice, 
        positions, edgePositions, pointPrimitives, text},
    stepTypes = Flatten[Permutations[#, {2}] & /@ {{0, 1}, {0, -1}}, 1];
    stepList = RandomChoice[stepTypes, steps];
    alternativeStep[currentPosition_, nextStep_] :=
      RandomChoice[Select[Complement[stepTypes, {nextStep}], (currentPosition + # ∈ region &)]];
    stepChoice[currentPosition_, nextStep_, nearEdgePosition_] :=
      If[currentPosition + nextStep ∈ region, 
        currentPosition + nextStep, 
        (Sow[nearEdgePosition];
         currentPosition + alternativeStep[currentPosition, nextStep])];
      {positions, edgePositions} = 
         FoldList[
           stepChoice[#1, Sequence @@ #2] &, 
           start, 
           MapIndexed[List, stepList]] // Reap;
      pointPrimitives[n_Integer] := 
        {If[MemberQ[Flatten @ edgePositions, n], Red, Black], 
         Point[positions[[n]]]};
      text[n_Integer] := 
        Text[
          Style[Row @ {n, ": ", positions[[n]]}, 
          If[MemberQ[Flatten @ edgePositions, n], Red, Black], Bold, 15], 
          {Right, Top}, {1., 1.}];
       Manipulate[
         Graphics[{
           Gray, region, AbsolutePointSize[5], 
           White, Line[positions], 
           pointPrimitives[i], 
           text[i]}, 
           Frame -> True, 
           ImagePadding -> 25], 
         {i, 1, Length[positions], 1}]]

randomWalk[500, {12, 12}, Rectangle[{0, 0}, {25, 25}]]

closely related: Sample of the random times at which the random walk crosses the boundary — Kuba, Jan 24 '16 at 23:40

score 7 · Answer 1 · answered Jan 24 '16 at 06:30

You could use Region functionality (for simpler regions), e.g.

rw[pt_, s_, n_, reg_] := 
 Module[{ch = {{0, 0}, {1, 0}, {-1, 0}, {0, 1}, {0, -1}}, np, st},
  st = RandomChoice[ch, n];
  FoldList[If[RegionMember[reg, #1 + s #2], #1 + s #2, #1] &, pt, st]
  ]
an[p_, step_, num_, regn_] := 
 With[{pnts = rw[p, step, num, regn]}, 
  ListAnimate[
   Graphics[{White, EdgeForm[Blue], regn, Black, Line[pnts[[1 ;; #]]],
        Red, PointSize[0.03], Point[pnts[[#]]]}] & /@ Range[2, num]]]

In the above the walker sticks (if proposed step goes outside region) till a direction (up, down,left, right) within region arises. Periodicity at boundary could be deal with withMod with offset.

Manipulate[
 an[{0, 1}, step, number, 
  region], {step, {0.05, 0.1, 0.2, 0.4}}, {number, {10, 100, 200, 
   500}}, {{region, 
   Disk[{1/2, 1/2}, 
    2]}, # -> 
     Graphics[#] & /@ {Polygon[{{-1, -1}, {1, -1}, {3, 3/2}, {2, 
       2}, {1, 1}, {-1, 2}, {0, 0}}], Disk[{1/2, 1/2}, 2], 
    Rectangle[{-1, -1}, {1, 2}]}}]

You could also use DiscreteMarkovProcess. In the following it is a random walk on a square grid with allowed moves includes not moving with each acceptable move equiprobable, e.g. upper left corner moves: +{0,0},+{1,0},+{0,1}->1/3.

func[num_, n_] := 
 If[Mod[num, n] == 0, {Quotient[num, n], n }, 
  QuotientRemainder[num, n] + {1, 0}]
f[lst_, n_] := Cases[lst, {_?(1 <= # <= n &), _?(1 <= # <= n &)}]

arr[n_] := 
 Module[{r = Range[n^2], 
   m = {{0, 0}, {1, 0}, {0, 1}, {-1, 0}, {0, -1}}, pos, mv, w, u},
  pos = func[#, n] & /@ r;
  mv = Map[Function[x, Union[# + x & /@ m]], pos];
  w = f[#, n] & /@ mv;
  u = Map[n (#[[1]] - 1) + #[[2]] &, w, {2}];
  SparseArray[
   Join @@ MapIndexed[
     Map[Function[x, {#2[[1]], x} -> 1/Length[#1]], #1] &, u], {n^2, 
    n^2}]
  ]

dm[n_, s_] := 
 Module[{mk = DiscreteMarkovProcess[1, arr[n]], rnd, p, sa, ap1, ap2},
  rnd = RandomFunction[mk, {0, s}];
  p = func[#, n] & /@ rnd["Values"];
  sa = SparseArray[p[[#]] -> 1, {n, n}] & /@ Range[s + 1];

  ap1 = MatrixPlot[#, Mesh -> All, 
      ColorRules -> {1 -> Black, 0 -> White}] & /@ sa; 
  ap2 = ListPlot[{-1/2, n + 1/2} + {1, -1} # & /@ 
       Reverse /@ (p[[1 ;; #]]), Joined -> True, 
      PlotStyle -> {Red, Thick}] & /@ Range[s + 1];
  Show @@@ Thread[{ap1, ap2}]]

Visualizing:

ListAnimate[dm[8, 200]]

I hope this is helpful or motivates. These are just "top of head" and neither pretty nor efficient but may prompt experts or other useful ideas.

score 3 · Accepted Answer · edited Jun 16 '20 at 09:23

Here are solutions to both boundary protocols. They are built on the same basic framework -- mainly the function that generates the moves for the walker is what differs between the two. There is a little adjustment in the way the lines and walker point is drawn because of discontinuities in the path generated by the wrap-arround protocol,

Path clips at the boundary

ClippingRandomWalk[
    steps_Integer,
    start : {_Integer, _Integer},
    rect : Rectangle[{xmin_, ymin_}, {xmax_, ymax_}]] /; start ∈ rect := 
  DynamicModule[{walk, next, positions},
    next[{x_, y_}] :=
      Module[{dx, dy},
        {dx, dy} = RandomChoice[{{-1, 0}, {1, 0}, {0, 1}, {0, -1}}];
        {Clip[x + dx, {xmin, xmax}], Clip[y + dy, {ymin, ymax}]}];
    walk[n_] := NestList[next, start, n];
    positions = walk[steps];
    Manipulate[
      Column[{
        Style[
          Row @ {"step: ", i, Spacer[20], "position: ", positions[[i + 1]]},
          "SB", 12],
        Graphics[{
          Gray, Scale[rect, 1.02],
          White, Thick, Line[positions],
          Red, PointSize[Large], Point[positions[[i + 1]]]},
          PlotRange -> {{xmin, xmax}, {ymin, ymax}},
          Frame -> True,
          PlotRangePadding -> Scaled[.025],
          ImageSize -> 400]}],
      Style["Clipping Random Walk", 12, "SB"],
      {{i, 0, Style["step", "SB", 11]}, 0, steps, 1, 
        Appearance -> "Open", ImageSize -> Large}]]
SeedRandom[4];
 ClippingRandomWalk[100, {1, 0}, Rectangle[{-5, -4}, {5, 4}]]

Path wraps to opposite side at the boundary

WrappingRandomWalk[
    steps_Integer,
    start : {_Integer, _Integer},
    rect : Rectangle[{xmin_, ymin_}, {xmax_, ymax_}]] /; start ∈ rect := 
  DynamicModule[{next, walk, pts, lines},
    next[{x_, y_}] := next[{{x, y}, {x, y}}];
    next[{{_, _}, pt : {x_, y_}}] :=
      Module[{nx, ny},
        {nx, ny} = pt + RandomChoice[{{-1, 0}, {1, 0}, {0, 1}, {0, -1}}];
        Which[
          nx < xmin, {{xmax, y}, {xmax - 1, y}},
          nx > xmax, {{xmin, y}, {xmin + 1, y}},
          ny < ymin, {{x, ymax}, {x, ymax - 1}},
          ny > ymax, {{x, ymin}, {x, ymin + 1}},
          True, {pt, {nx, ny}}]];
    walk[n_] := NestList[next, start, n] // Rest; 
    With[{w = walk[steps]},
      pts = Prepend[w[[All, 2]], start];
      lines = Line /@ w];
    Manipulate[
      Column[{
        Style[
          Row @ {"step: ", i, Spacer[20], "position: ", pts[[i + 1]]}, 
          "SB", 12],
        Graphics[{
          Gray, Scale[rect, 1.02],
          White, Thick, lines,
          Red, PointSize[Large], Point[pts[[i + 1]]]},
          PlotRange -> {{xmin, xmax}, {ymin, ymax}},
          Frame -> True,
          PlotRangePadding -> Scaled[.025],
          ImageSize -> 400]}],
      Style["Wrapping Random Walk", 12, "SB"],
      {{i, 0, Style["step", "SB", 11]}, 0, steps, 1, 
        Appearance -> "Open", ImageSize -> Large}]]
SeedRandom[4];
WrappingRandomWalk[100, {1, 0}, Rectangle[{-5, -4}, {5, 4}]]

Confining/Periodic boundary conditions implementation for 2D Random Walker

2 Answers2

Path clips at the boundary

Path wraps to opposite side at the boundary