5

How could we display the position of any sub expression in an expression using Tooltip?

This would be useful for example in order to locate the position of an element in the FullForm of a Plot.

I think I saw a similar Q&A once, but I haven't found it again.

Edit

The answer of Kuba is very instructive. Here is the function I had in mind which is a variation of Kuba's answer.

labelPositions[graphics_] := Fold[Function[{plot, pos}, MapAt[Tooltip[#, pos] &, plot, pos]], graphics, Position[graphics,_,Infinity]]

Using Kuba's comment, even simpler

labelPositions[graphics_]:= MapIndexed[Tooltip,graphics,Infinity, Heads -> True]
faysou
  • 10,999
  • 3
  • 50
  • 125

1 Answers1

5

We have to use Is there a GraphicsPrimitiveQ (or a complete list of Heads of graphics primitives)?

primitivesQ = MatchQ[#, 
    Alternatives @@ {Point, PointBox, Line, LineBox, Arrow, ArrowBox,           Rectangle, RectangleBox, Parallelogram, Triangle, JoinedCurve,           JoinedCurveBox, FilledCurve, FilledCurveBox, StadiumShape,           DiskSegment, Annulus, BezierCurve, BezierCurveBox, BSplineCurve,           BSplineCurveBox, BSplineSurface, BSplineSurface3DBox,           SphericalShell, CapsuleShape, Raster, RasterBox, Raster3D,           Raster3DBox, Polygon, PolygonBox, RegularPolygon, Disk, DiskBox,           Circle, CircleBox, Sphere, SphereBox, Ball, Ellipsoid,           Cylinder, CylinderBox, Tetrahedron, TetrahedronBox, Cuboid,           CuboidBox, Parallelepiped, Hexahedron, HexahedronBox, Prism,           PrismBox, Pyramid, PyramidBox, Simplex, ConicHullRegion,           ConicHullRegionBox, Hyperplane, HalfSpace, AffineHalfSpace,           AffineSpace, ConicHullRegion3DBox, Cone, ConeBox, InfiniteLine,           InfinitePlane, HalfLine, InfinitePlane, HalfPlane, Tube, 
      TubeBox, GraphicsComplex, GraphicsComplexBox, GraphicsGroup,           GraphicsGroupBox, GeoGraphics, Graphics, GraphicsBox,           Graphics3D, Graphics3DBox, MeshRegion, BoundaryMeshRegion,           GeometricTransformation, GeometricTransformationBox, Rotate,           Translate, Scale, SurfaceGraphics, Text, TextBox, Inset,           InsetBox, Inset3DBox, Panel, PanelBox, Legended, Placed,           LineLegend, Texture}
    ] &;

code

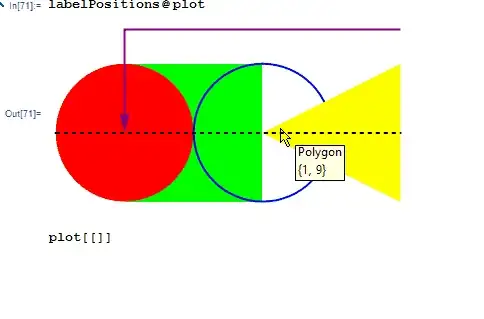
labelPositions[graphics_] := Fold[
  Function[{plot, pos}, 
   MapAt[Tooltip[#, Column@{Head[#], pos}] &, plot, pos]],
  graphics,
  Position[graphics, x_[___] /; primitivesQ[x], \[Infinity]]
  ]

test

plot = Graphics[{Thick, Green, Rectangle[{0, -1}, {2, 1}], Red, 
    Disk[], Blue, Circle[{2, 0}], Yellow, 
    Polygon[{{2, 0}, {4, 1}, {4, -1}}], Purple, Arrowheads[Large], 
    Arrow[{{4, 3/2}, {0, 3/2}, {0, 0}}], Black, Dashed, 
    Line[{{-1, 0}, {4, 0}}]}];


labelPositions @ plot

enter image description here

todo

This is done with an assumption that primitives are not nested within others. In general that's not true, like for FilledCurve @ BSplineCurve[...] so those cases should be handled with more care.

Community
  • 1
Kuba
  • 136,707
  • 13
  • 279
  • 740
  • This is very impressive. I modified your function to suit what I wanted, ie to get the position of any component of an expression represented in FullForm: labelPositions[graphics_] := Fold[Function[{plot, pos}, MapAt[Tooltip[#, pos] &, plot, pos]], graphics, Position[graphics, x_, Infinity]] – faysou Jan 25 '16 at 22:45
  • I realized with your answer, it would be quite practical if MapAt had the position in #2 as argument similarly to MapIndexed. Maybe one day, or maybe not, as maybe this could have an impact on performance, I don't know. – faysou Jan 26 '16 at 08:43
  • @faysou yep, but what about: `MapIndexed[If[#2[[-1]] == 0, Tooltip[##], #] &,

    plot , {1, [Infinity]}, Heads -> True]`

     – Kuba Jan 26 '16 at 08:48
  • Looks good ! Thanks – faysou Jan 26 '16 at 23:16