Creating a cloud of blocks that form I ♥ U in different viewpoints

Question

This picture shown bellow has three shapes with different view angle (I ♥ U). How to do this type of model? A few tries:

With[{p=Position[ImageData[Binarize[Rasterize[#, ImageSize -> 10]]], 0]},
    Graphics3D[Cuboid /@ PadRight[p, {Length@p, 3}, 0]]
   ] & /@ {"I", "♥", "U"}

Answer 1

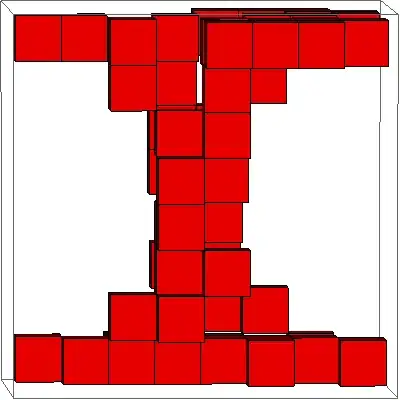
tl;dr

Playing with your code I found that using Rasterize is a mayor pain in the behind because of various reasons (RasterSize is, at least for me, not working as advertised in the documentation; I found no easy way to remove padding around letters and get a nice $n \times n$ representation of each letter, get each letter the appropriate size, issues with different fonts etc.)

So instead I googled for a 8-bit letter generator and created letters of my own. A bit of copy-paste and string-manipulation in Mathematica and I got the following letter representation:

i = {{1,1,1,1,1,1,1,1},
     {0,0,0,1,1,0,0,0},
     {0,0,0,1,1,0,0,0},
     {0,0,0,1,1,0,0,0},
     {0,0,0,1,1,0,0,0},
     {0,0,0,1,1,0,0,0},
     {0,0,0,1,1,0,0,0},
     {1,1,1,1,1,1,1,1}}

u = {{1,1,1,0,0,1,1,1},
     {0,1,0,0,0,1,1,0},
     {0,1,0,0,0,1,1,0},
     {0,1,0,0,0,1,1,0},
     {0,1,0,0,0,1,1,0},
     {0,1,0,0,0,1,1,0},
     {0,1,1,0,0,1,1,0},
     {0,0,1,1,1,1,0,0}}

and (with some artistic freedom):

h = {{0,0,1,0,0,0,1,0},
     {0,1,1,1,0,1,1,0},
     {1,1,1,1,1,1,1,1},
     {0,1,1,1,1,1,1,1},
     {0,0,1,1,1,1,1,1},
     {0,0,0,1,1,1,1,0},
     {0,0,0,0,1,1,1,0},
     {0,0,0,0,0,1,0,0}}

Helper functions:

1. The following function transforms a matrix of zeros and ones into positions where the matrix contains a one

   toIndex[matrix_]:= matrix 
                      //MapIndexed[If[#1==1,#2, Nothing[] ]&, #, {2}]& 
                      //Flatten[#,1]&
   

2. This function transforms a list of form {{x1, y1},...{x8, y8}} into {{x1, y1, z1}, {x1, y1, z2}} ... {x8, y8, z8}

   to3D[pos_]:= Table[pos /. {x_,y_}-> {x,y,z}, {z, 1, 8}] //Flatten[#,1]&
   

3. A wrapper for Cuboid to accept the center of the unit cube instead of the lower left corner as parameter

   toCube[center_]:= Cuboid[center-{0.5, 0.5, 0.5}]
   

Now lets create some graphics and save the position definitions in some symbols box1, box2 and box3 :

(box1=(i//toIndex//to3D) /.{x_,y_,z_}-> {y, z, x} ) //Map[toCube] //Graphics3D

(box2=(u//toIndex //to3D) /.{x_,y_,z_}-> {z, y, -x+9} ) //Map[toCube] //Graphics3D

(box3=(heart //toIndex//to3D) /.{x_,y_,z_}-> {x, y, z} ) //Map[toCube] //Graphics3D

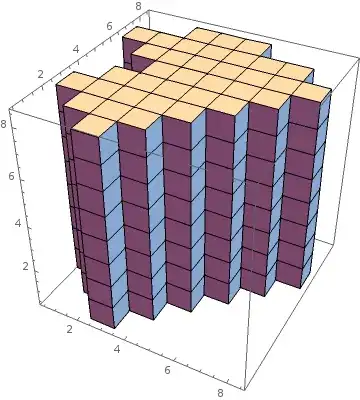
Note the coordinate transformation via replacement rules to get the right orientation

Finally we can assemble the whole thing via intersection:

Intersection[box1, box2, box3] //Map[toCube] //Graphics3D

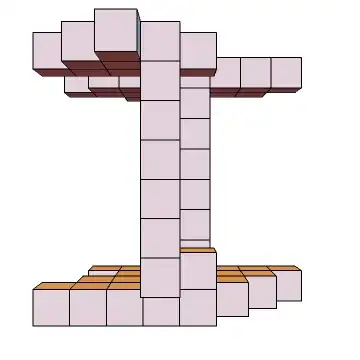
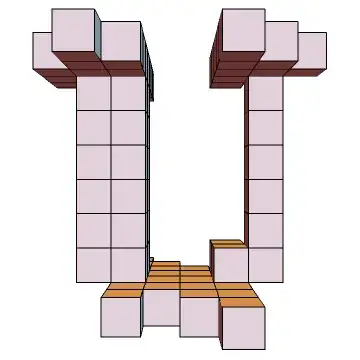
Edit:

As one can see my solution does not result in the kind of "random box-cloud" that the OP showed in his question. This is due to the intersection method that was used to "sculpt" the geometry. Here is an improved version that amends this:

The following function neighboursQ tests wether a block has neighbours. A neighbour is a block that shares one axis with the block in question. Only when it has neighbouring blocks to all sides can it be deleted without compromising the projection.

neighboursQ[list_][{x_,y_,z_}]:= {
                                   Cases[list, {_,y,z}],
                                   Cases[list, {x,_,z}],
                                   Cases[list, {x,y,_}]
                                 } //Map[Length] 
                                   //Subtract[#, 1]& 
                                   //MatchQ[{___,0,___}] 
                                   //Not

Let's test on two simple examples:

testbox = Table[{i, j, k}, {i, 1, 3}, {j, 1, 3}, {k, 1, 3}]  //Flatten[#,2]&
testbox2= DeleteCases[testcube, {2,1,1}|{3,1,1}|{1,1,2}]

testbox is a full $9 \times 9$ box so that we expect each block to have neighbours. We can confirm that via testbox //Map[neighboursQ[testbox]] which yields a whole bunch of True. Now on to testbox2:

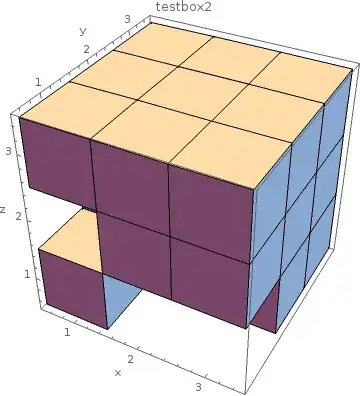
 neighboursQ[testcube2][{1,1,1}] (*False*)
 neighboursQ[testcube2][{1,1,3}] (*True*)

neighboursQ works as we saw in the examples so we just have to repeatedly (and randomly) apply it our blocks. I wrote the following function to do just that. (It gets applied 500 times via Nest so that it has a high chance to have found any remaining block with neighbours, your milage may vary depending on number of blocks to start with)

deleteDuplicates[list_]:= Nest[With[{this=RandomChoice@#},
If[neighboursQ[#][this], DeleteCases[#,this], #]]&, list, 500]

Some other random examples:

Grid[{{x,x},{x,x}}] 
/. x:>(Intersection[box1, box2, box3]  //deleteDuplicates //Map[toCube] //Graphics3D)