Weird behaviour for a vector InterpolatingFunction inside an NDSolve

Question

I have run into some weird behaviour on the part of NDSolve which I find pretty bizarre and which I would like to understand better.

Suppose, for the sake of argument, that I want to study the ODE system $$ \left\{\begin{array}{l} y'(x)=\cos(x)\phantom{y(x)}\\ z'(x)=y(x),\phantom{\cos(x)} \end{array}\right. $$ and that I want to do it sequentially. This is pretty easy: I begin by solving the first equation and setting the resulting InterpolatingFunction to a placeholder f,

f = y /. First[NDSolve[{y'[x] == Cos[x], y[0] == 0}, y, {x, 0, 20}]]

and then I use this f inside the second NDSolve,

NDSolve[{z'[x] == f[x], z[0] == 0}, z, {x, 0, 20}]

and everything is dandy.

Going a bit further down For The Sake Of Argument alley, suppose that for whatever reason I want my forcing functions and dependent variables to have vector values (with a single entry). I need to adjust the initial conditions to match, but otherwise everything works fine:

g = y /. First[NDSolve[{y'[x] == {Cos[x]}, y[0] == {0}}, y, {x, 0, 20}]]
NDSolve[{z'[x] == g[x], z[0] == {0}}, z, {x, 0, 20}]

Now finally, suppose that some devious, argumentative trickster decides to sneak in to change the g[x] and add a zero of appropriate dimensions, changing that right-hand side to {0}+g[x], so the command will look like

NDSolve[{z'[x] == {0} + g[x], z[0] == {0}}, z, {x, 0, 20}]

"That's not a problem!", I hear you say, "surely that's not something that will cause Mathematica to just suddenly throw its hands up in the air and give up, right?", and I wholeheartedly agree with you.

Unfortunately, that's not really the case. For some reason, that last bit seems to simply be too much, and Mathematica returns the whole NDSolve construct undigested:

Now this is pretty weird. Watering down the NDSolve commands to non-evaluating ndsolves throws some light into what's going on: when the arguments to the solver are processed, adding the explicit {0} to the symbolic g[x] results in the equation z'[x]=={g[x]}, where the right-hand side is one level too deep:

As such, putting in an explicit part statement on the g, or making the initial condition for z one level deeper will produce mostly acceptable results (or at least, it will produce results, but the second option gives the wrong shape). Thus

NDSolve[{z'[x] == {0} + g[x][[1]], z[0] == {0}}, z, {x, 0, 20}]
NDSolve[{z'[x] == {0} + g[x], z[0] == {{0}}}, z, {x, 0, 20}]

produces

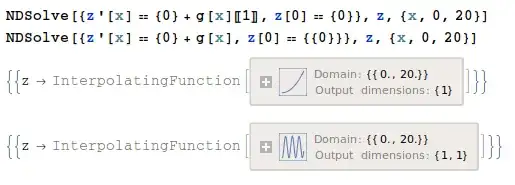
Now this is sort of acceptable (at least it sort of kind of fixes the problem) but it feels like a horrible kludge to me.

Mostly, though, I'm deeply uncomfortable with the fact that expressions which look equivalent (g[x] and {0}+g[x]) produce wildly different results, in an unstable, you-can't-know-what-you'll-get sort of way. Is there a unified way to ensure a more uniform output in this sort of situation?

Answer 1

@march pointed out the source of the issue:

I think this is the same as {a} + b == {a + b}, where b is your InterpolatingFunction object. If List is not the Head of b, then Plus, being Listable will absorb that b into List[a]. I'm betting there is probably no getting around this. – march Feb 3 '16 at 22:22

The OP presents a workaround that is a bit unsatisfactory in that the array depth of the result is increased unnecessarily. I'll present a different workaround that avoids this. The difficulty can be averted if we can prevent lists/vectors being combined with expressions that do not evaluate to lists until x is numeric. In other words, we have to protect vector-valued expressions from evaluating to lists until x is numeric.

g = y /. First[NDSolve[{y'[x] == {Cos[x]}, y[0] == {0}}, y, {x, 0, 20}]]
const[x_?NumericQ] := {0};
NDSolve[{z'[x] == const[x] + g[x], z[0] == {0}}, z, {x, 0, 20}]