4

I have used the following code to generate eigenfunctions of a PDE:

{vals, funs} = 
  NDEigensystem[{-Laplacian[u[x, y], {x, y}], 
    DirichletCondition[u[x, y] == 0, True]}, 
   u[x, y], {x, y} \[Element] 
    Polygon[{{-1/2, -1/2}, {1/2, -1/2}, {1/2, 1/2}, {-1/2, 1/2}}], 4];

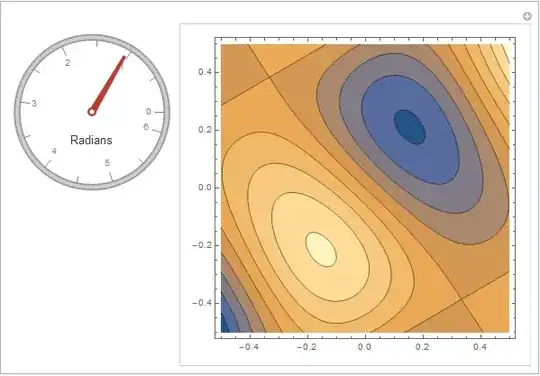
By applying funs[[3]]you can see that the third eigenfunction is an interpolating function:

Interpolating Function

With contour plot:

Plot of third eigenfunction

What I now wish to do is to transform this function by rotating it anticlockwise by $\frac{\pi}{2}$ about the origin.

Let's say that the points lying on our eigenfunction are $(x,y,f(x,y))$.

I now wish to effectively move these points by perhaps taking $(x,y) \mapsto (y,-x)$

I cannot seem to find anything online to describe how to do this for these interpolating functions.

I tried defining a function R and applying it to funs[[3]] with no success. 

R := Function[g, g /. Thread[{x, y} -> ({y,-x})]]

I thought that this may work as it would replace the coordinates for me, but I now know that my logic is flawed.

Please note: I am not asking how to rotate the contourplot (even though a contour plot of the transformed eigenfunction should look identical to it) I would like a transformation to be applied to the function because I intend to use it later on.

I would be really grateful if somebody could help me on this - I've been playing around with code for the past three hours.

user21
  • 39,710
  • 8
  • 110
  • 167
Mr S 100
  • 711
  • 6
  • 11
  • Can't test on mobile, but what about simply f[y, - x]? Where f is the initial interpolating function. – LLlAMnYP Feb 03 '16 at 23:42
  • Doing so doesn't give off an error but the contour plot is blank. This might be my fault though - I'm very new to mathematica. – Mr S 100 Feb 03 '16 at 23:54
  • There's nothing wrong with your approach (with is essentially from my answer here), as you can see by calling R[funs[[1]]]. You just have to watch out whether you have an object with Head of InterpolationFunction or not. What your solver returns is an interpolating function, evaluated at a symbolic argument (not the actual function!). In rotating it, you have to replace the symbolic arguments by rotated versions. For what you're after, it may be better to change NDEigensystem by replacing u[x,y] with u in argument 2. – Jens Feb 04 '16 at 00:30

2 Answers2

8

You can use RotationTransform.

With[{rot = funs[[3]] /. Inner[Rule, {x, y}, RotationTransform[π/2][{x, y}], List]},
 ContourPlot[rot, {x, -.5, .5}, {y, -.5, .5}]
]

enter image description here

Hope this helps.

Also with Manipulate

Manipulate[
 With[{rot = funs[[3]] /. Inner[Rule, {x, y}, RotationTransform[θ][{x, y}], List]},
  Quiet@ContourPlot[rot, {x, -.5, .5}, {y, -.5, .5}]],
 Column[{
   AngularGauge[Dynamic@θ, {0, 2 π}, 
    ScaleOrigin -> {0, 2 π}, ScaleDivisions -> {8, 2}, 
    TargetUnits -> "Radians", GaugeLabels -> "Radians"]}],
 ControlPlacement -> Left
 ]

enter image description here

Edmund
  • 42,267
  • 3
  • 51
  • 143
6
rotation = {x, y}.{{Cos[t], Sin[t]}, {-Sin[t], Cos[t]}};
f[t_] = funs[[3]] /. {x -> rotation[[1]], y -> rotation[[2]]};
Manipulate[
 ContourPlot[f[t], {x, -.3, .3}, {y, -.3, .3}], {t, -\[Pi], \[Pi]}]

enter image description here

Basheer Algohi
  • 19,917
  • 1
  • 31
  • 78
  • This looks really good but unfortunately I keep getting the error 'Tag Plus in (Sin[x]+Sin[y])[t_] is Protected'. What am I doing wrong? – Mr S 100 Feb 03 '16 at 23:55
  • You have a definition of f before. Clear[f] or used different symbol. – Basheer Algohi Feb 03 '16 at 23:57
  • Silly me - you were right! It's all working now. Could I ask why you've indexed as rotation[[1]] and rotation[[2]]? Thanks – Mr S 100 Feb 04 '16 at 00:05
  • rotation is a vector and the first component has to be in position of x and the second component has to be in position of y (look at the [x,y] at the end of your function). – Basheer Algohi Feb 04 '16 at 00:10