4

I'm solving numerically a system of differential equations with the use of NDSolve. The numerical integration works only a very small interval of the argument.

I'm wondering if anyone could help me with finding better settings for NDSolve.

ClearAll["Global`*"];

(* THE EXACT SOLUTIONS ARE KNOWN ONLY FOR THE CERTAIN VALUES OF THE PARAMETERS *)
{λ, β, γ, μ, v} = {1, 433/2116, 1, 23/25, 1};
{α, A} = {(8 Sqrt[3])/25, (23 Sqrt[2])/25};

(* THEY ARE USED FOR SETTING BOUNDARY CONDITIONS *)
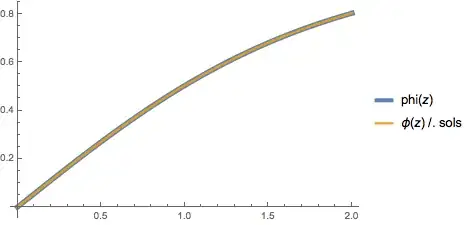
phi[z_] = v*Tanh[α*z];
chi[z_] = A/Cosh[α*z];

(* THE INTERVAL: HERE'S THE PROBLEM *)
zmin = 0;
(* !!! CHANGE 1.5 TO 2 AND THE SOLVING WILL FAIL !!!*)
zmax = 1.5;

sols = NDSolve[{
   D[ϕ[z], z, z] == 4*λ*ϕ[z]*(ϕ[z]*ϕ[z] - v^2) + 2*γ*χ[z]*χ[z]*ϕ[z],
   D[χ[z], z, z] == 2*γ*χ[z]*(ϕ[z]*ϕ[z] - μ^2) + 4*β*γ*χ[z]*χ[z]*χ[z],
   ϕ[zmin] == phi[zmin],
   ϕ[zmax] == phi[zmax],
   χ[zmin] == chi[zmin],
   χ[zmax] == chi[zmax]
   }, {ϕ, χ}, {z, zmin, zmax}
  ]

Plot[{phi[z], ϕ[z] /. sols}, {z, zmin, zmax},
PlotStyle -> {Thickness[0.015], Thickness[0.007]},
PlotLegends -> "Expressions"]

Plot[{chi[z], χ[z] /. sols}, {z, zmin, zmax},
PlotStyle -> {Thickness[0.015], Thickness[0.007]},
PlotLegends -> "Expressions"]

Many thanks!!

mavzolej
  • 693
  • 4
  • 10
  • Welcome to Mathematica.SE!
    1. As you receive help, try to give it too, by answering questions in your area of expertise.
    2. Take the tour and check the faqs!
    3. When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge.

    Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign!

     –  Feb 05 '16 at 07:26
  • The given system seems to have singularities at z = 0.73 and around z = 1.4 (and may be in other places too). I would try setting MaxSteps -> Infinity and also try with WorkingPrecision option. Or may be you can split the solution range by skipping these singular points, I mean solve for values of z to be from 0 to 0.73 and 0.74 to 1.4 and so on... – Lotus Feb 05 '16 at 11:37
  • Thanks for an immediate response!

    Well, I'd rather call these points pseudosingularities, since the equation is solved perfectly for an arbitrary interval covering them, if this interval is small enough. Say, [0, 1] or [1, 2]. Also, the solutions themselves look pretty smooth and nice...

    Do you know by any chance how to set the mesh manually? For example, by fixing the number of points and setting them equidistant.

    Or, even better, how to define the mesh as an array and then transfer in to NDSolve.

     – mavzolej Feb 05 '16 at 15:19

1 Answers1

4

Sometimes a manual approach to the shooting method makes a BVP easier to solve.

Set up with ParametricNDSolveValue:

zmin = 0;
zmax = 2;

psol = ParametricNDSolveValue[{
    D[ϕ[z], z, z] == 4*λ*ϕ[z]*(ϕ[z]*ϕ[z] - v^2) + 2*γ*χ[z]*χ[z]*ϕ[z], 
    D[χ[z], z, z] == 2*γ*χ[z]*(ϕ[z]*ϕ[z] - μ^2) + 4*β*γ*χ[z]*χ[z]*χ[z],
    ϕ[zmin] == phi[zmin], ϕ'[zmin] == phip,
    χ[zmin] == chi[zmin], χ'[zmin] == chip},
   {ϕ, χ}, {z, zmin, zmax}, {phip, chip}];

Manual shooting method:

obj[p_?NumericQ, c_?NumericQ] := Through[psol[p, c][zmax]];
solpc = FindRoot[obj[p, c] == {phi[zmax], chi[zmax]}, {{p, 0.5}, {c, 0.}}]
(*  {p -> 0.554256, c -> 2.47664*10^-8}  *)

sols = Thread[{ϕ, χ} -> psol[p, c] /. solpc];
{ϕ[zmax] - phi[zmax], χ[zmax] - chi[zmax]} /. sols
(*  {1.87628*10^-14, 1.85407*10^-14}  *)

Plots:

Plot[{phi[z], ϕ[z] /. sols}, {z, zmin, zmax}, 
 PlotStyle -> {Thickness[0.015], Thickness[0.007]}, 
 PlotLegends -> "Expressions"]

Plot[{chi[z], χ[z] /. sols}, {z, zmin, zmax}, 
 PlotStyle -> {Thickness[0.015], Thickness[0.007]}, 
 PlotLegends -> "Expressions"]

Mathematica graphics

Mathematica graphics

Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Thanks for a great idea! This indeed helps to slightly increase the interval for which the equation can be solved. However, it is still not working for regions like [-5,5] and reporting about singularities :(

    It works slightly better if we enter the exact values of the derivatives but still diverges at some point. So, the system seems to be very unstable.

    Doesn't it mean that it would be good to solve it on a fixed mesh by some method which constructs a large matrix and immediately takes into account both boundary conditions? I just don't know how to implement this :(

     – mavzolej Feb 06 '16 at 06:05
  • 1
    Such a method was one of the solutions presented here: http://mathematica.stackexchange.com/questions/91854/nonlinear-differential-equation-numerical-solution/97733#97733 – Michael E2 Feb 06 '16 at 13:36