I want to have two groups of $n$ random numbers $u_i$ and $v_i$ in $U(0,1)$, such that $\sum u_i = \sum v_i$
What I tried is:
I can firstly get $u_i$ by RandomReal[{0,1},n], make $s=\sum u_i$.
Then I found it is very difficult to generate another $n$ uniformly distributed random numbers $v_i$ from $U(0,1)$ that sum to $s$, where $s$ is a real value in $[0,n]$. I can scale it but need to reject many cases that $v_i$ is larger than 1, I guess.
Try to make the question clearer, my original problem is:
I have $8$ parameters $\kappa_i, i=1,\ldots,8$ from a system, each parameter $\kappa_i$ can be any value in $[0,1]$. But I have a constraint on my parameters which is $\kappa_1+\kappa_2+\kappa_3+\kappa_4=\kappa_5+\kappa_6+\kappa_7+\kappa_8$. Now I want to sample the whole parameter space (is this counted as Monte Carlo?) with such constraint. What should I do?
Update:
I have used @Coolwater 's method, but the problem is that rejecting any values larger than 1 costs a lot. When I want to sample 10,000 sets, it costs me hours. By the time I update this post, it is still running.
Any ideas about how to do this efficiently?
More update: @JasonB 's approach perfectly solved my problem. Actually, it makes sense that just scale the larger group based on the two sums ratio!!! I was too stupid to come out with this idea, which is very intuitive and straightforward!
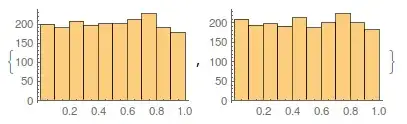

RandomReal; then generate the 2nd by permuting the 1st one. – m_goldberg Feb 06 '16 at 10:06