Faster way to test possible points-to-plane-fitting identity?

Question

Summary: I want to confirm the three sum-defined quantities in https://github.com/barrycarter/bcapps/blob/master/STACK/planetest.m (also below) are identically zero for all values of n>=3.

While attempting to solve https://stats.stackexchange.com/questions/196655 (fitting points to a plane), I came up with these (probably either wrong or previously derived by someone else) formulas for a,b,c such that z=a*x+b*y+c is a best fit for n points x[i], y[i], and z[i]:


a = 
-((Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
   Sum[x[i], {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
   Sum[y[i], {i, 1, n}]^2*Sum[x[i]*z[i], {i, 1, n}] + 
   n*Sum[y[i]^2, {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] + 
   Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}] - 
   n*Sum[x[i]*y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])/
  (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 
   2*Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
   n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
    Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]))

b =
-((-(Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}]) + 
   Sum[x[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}] + 
   Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] - 
   n*Sum[x[i]*y[i], {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] - 
   Sum[x[i], {i, 1, n}]^2*Sum[y[i]*z[i], {i, 1, n}] + 
   n*Sum[x[i]^2, {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])/
  (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 
   2*Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
   n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
    Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]))

c =
(Sum[x[i]*y[i], {i, 1, n}]^2*Sum[z[i], {i, 1, n}] - 
  Sum[x[i]^2, {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
  Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] + 
  Sum[x[i], {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] + 
  Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}] - 
  Sum[x[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])/
 (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 
  2*Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
  n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
   Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*Sum[y[i]^2, {i, 1, n}])

To confirm these values, I'd compute the sum of the differences squared. Each term would look like this:

diff[i_] = (z[i]-(a*x[i]+b*y[i]+c))^2

Treating the sum as a function of a,b,c, I would take partials with respect to these three variables and set equal to 0.

Since derivatives add, I would be adding the sum of the derivatives of each term:


derva[i_] = -2*x[i]*(-c - a*x[i] - b*y[i] + z[i])
dervb[i_] = -2*y[i]*(-c - a*x[i] - b*y[i] + z[i])
dervc[i_] = -2*(-c - a*x[i] - b*y[i] + z[i])

and setting each sum equal to 0.

Mathematica won't solve that for arbitrary n (which I sort of expected):


Solve[{
 Sum[derva[i],{i,1,n}] == 0,
 Sum[dervb[i],{i,1,n}] == 0,
 Sum[dervc[i],{i,1,n}] == 0
}, {a,b,c}]

Out[74] = {}

and Reduce doesn't help either. Keeping the derivative outside the sum doesn't work either, albeit with a different error message (the standard Solve::nsmet: This system cannot be solved with the methods available to Solve.).

Mathematica will solve for a,b,c for specific values of n, which led me to the guess above.

To test my guess, I need to confirm that each partial derivative is zero. In other words, I need to confirm:


Sum[-2*x[i]*(-c - a*x[i] - b*y[i] + z[i]),{i,1,n}] == 0
Sum[-2*y[i]*(-c - a*x[i] - b*y[i] + z[i]),{i,1,n}] == 0
Sum[-2*(-c - a*x[i] - b*y[i] + z[i]),{i,1,n}] == 0

are identically zero for all values of x[i], y[i], z[i], and n, when I put in my guesses above.

In other words (these are the big ugly equations which I'm intentionally giving in "full" form for those who don't want to read the rest of this question)...:


atest[n_] := 

Sum[-2*x[i]*(-((Sum[x[i]*y[i], {i, 1, n}]^2*Sum[z[i], {i, 1, n}] - 
      Sum[x[i]^2, {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
      Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*
       Sum[x[i]*z[i], {i, 1, n}] + Sum[x[i], {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*
       Sum[x[i]*z[i], {i, 1, n}] + Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]*
       Sum[y[i]*z[i], {i, 1, n}] - Sum[x[i], {i, 1, n}]*
       Sum[x[i]*y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])/
     (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 2*Sum[x[i], {i, 1, n}]*
       Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
      n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
       Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*
       Sum[y[i]^2, {i, 1, n}])) + 
   ((Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
      Sum[x[i], {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
      Sum[y[i], {i, 1, n}]^2*Sum[x[i]*z[i], {i, 1, n}] + 
      n*Sum[y[i]^2, {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] + 
      Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}] - 
      n*Sum[x[i]*y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])*x[i])/
    (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 
     2*Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
     n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
      Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*
      Sum[y[i]^2, {i, 1, n}]) + 
   ((-(Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}]) + 
      Sum[x[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}] + 
      Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] - 
      n*Sum[x[i]*y[i], {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] - 
      Sum[x[i], {i, 1, n}]^2*Sum[y[i]*z[i], {i, 1, n}] + 
      n*Sum[x[i]^2, {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])*y[i])/
    (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 
     2*Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
     n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
      Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*
     Sum[y[i]^2, {i, 1, n}]) + z[i]), {i, 1, n}];

btest[n_] :=

Sum[-2*y[i]*(-((Sum[x[i]*y[i], {i, 1, n}]^2*Sum[z[i], {i, 1, n}] - 
      Sum[x[i]^2, {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
      Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*
       Sum[x[i]*z[i], {i, 1, n}] + Sum[x[i], {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*
       Sum[x[i]*z[i], {i, 1, n}] + Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]*
       Sum[y[i]*z[i], {i, 1, n}] - Sum[x[i], {i, 1, n}]*
       Sum[x[i]*y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])/
     (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 2*Sum[x[i], {i, 1, n}]*
       Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
      n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
       Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*
       Sum[y[i]^2, {i, 1, n}])) + 
   ((Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
      Sum[x[i], {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
      Sum[y[i], {i, 1, n}]^2*Sum[x[i]*z[i], {i, 1, n}] + 
      n*Sum[y[i]^2, {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] + 
      Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}] - 
      n*Sum[x[i]*y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])*x[i])/
    (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 
     2*Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
     n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
      Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*
      Sum[y[i]^2, {i, 1, n}]) + 
   ((-(Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}]) + 
      Sum[x[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}] + 
      Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] - 
      n*Sum[x[i]*y[i], {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] - 
      Sum[x[i], {i, 1, n}]^2*Sum[y[i]*z[i], {i, 1, n}] + 
      n*Sum[x[i]^2, {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])*y[i])/
    (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 
     2*Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
     n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
      Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*
      Sum[y[i]^2, {i, 1, n}]) + z[i]), {i, 1, n}];

ctest[n_] :=

Sum[-2*(-((Sum[x[i]*y[i], {i, 1, n}]^2*Sum[z[i], {i, 1, n}] - 
      Sum[x[i]^2, {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
      Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*
       Sum[x[i]*z[i], {i, 1, n}] + Sum[x[i], {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*
       Sum[x[i]*z[i], {i, 1, n}] + Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]*
       Sum[y[i]*z[i], {i, 1, n}] - Sum[x[i], {i, 1, n}]*
       Sum[x[i]*y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])/
     (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 2*Sum[x[i], {i, 1, n}]*
       Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
      n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
       Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*
       Sum[y[i]^2, {i, 1, n}])) + 
   ((Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
      Sum[x[i], {i, 1, n}]*Sum[y[i]^2, {i, 1, n}]*Sum[z[i], {i, 1, n}] - 
      Sum[y[i], {i, 1, n}]^2*Sum[x[i]*z[i], {i, 1, n}] + 
      n*Sum[y[i]^2, {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] + 
      Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}] - 
      n*Sum[x[i]*y[i], {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])*x[i])/
    (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 
     2*Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
     n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
      Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*
      Sum[y[i]^2, {i, 1, n}]) + 
   ((-(Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}]) + 
      Sum[x[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}]*Sum[z[i], {i, 1, n}] + 
      Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] - 
      n*Sum[x[i]*y[i], {i, 1, n}]*Sum[x[i]*z[i], {i, 1, n}] - 
      Sum[x[i], {i, 1, n}]^2*Sum[y[i]*z[i], {i, 1, n}] + 
      n*Sum[x[i]^2, {i, 1, n}]*Sum[y[i]*z[i], {i, 1, n}])*y[i])/
    (Sum[x[i]^2, {i, 1, n}]*Sum[y[i], {i, 1, n}]^2 - 
     2*Sum[x[i], {i, 1, n}]*Sum[y[i], {i, 1, n}]*Sum[x[i]*y[i], {i, 1, n}] + 
     n*Sum[x[i]*y[i], {i, 1, n}]^2 + Sum[x[i], {i, 1, n}]^2*
      Sum[y[i]^2, {i, 1, n}] - n*Sum[x[i]^2, {i, 1, n}]*
      Sum[y[i]^2, {i, 1, n}]) + z[i]), {i, 1, n}];

I'm claiming atest[n], btest[n], ctest[n] are identially 0 for all values of n>=3.

How far I've gotten on my own:



t = Table[Simplify[{atest[i], btest[i], ctest[i]}], {i,3,6}]

Out[1]= {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}, {0, 0, 0}}

However, Simplify[atest[7]] just hangs. Even if I waited for it, I suspect Simplifying atest, btest, and ctest for larger numbers would take even longer.

I realize I'm asking Mathematica to do a lot, especially since I'm using symbols instead of actual numbers, but is there a good way to verify this identity for all n>=3 (or prove its false, of course).

For anyone interested, https://github.com/barrycarter/bcapps/blob/master/STACK/bc-solve-stats-196655.m has some notes re how I 'derived' this.

You can make headway by exploiting the linearity of a sum: $\sum_i (ax_i+by_i)=a\sum_i x_i+b\sum_i y_i$. — J. M.'s missing motivation, Feb 15 '16 at 18:14
I wonder if any of the results shown here may help you: http://www.geometrictools.com/Documentation/LeastSquaresFitting.pdf — MarcoB, Feb 15 '16 at 18:20
@MarcoB That's what the OP of the linked post found and was confused by. It involves matrix equations (as does every other solution I've found) and he's looking for a closed form. I'd be surprised if I'd actually discovered one, but maybe I have. — , Feb 15 '16 at 18:25
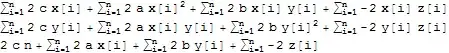
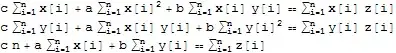
I guess that my underlying question would then be: what is the advantage of dealing with a closed form answer, when it is much more expedient to carry out the calculation numerically with the actual points you have at hand? If you imagine that your point coordinates are in a list called points, then this one-liner will give you the best approximations for $(a, b, c)$: Solve[Grad[Total[(a #1 + b #2 + c - #3)^2 & @@@ points], {a, b, c}] == 0, {a, b, c}]. Can you not use those to do any further checking? — MarcoB, Feb 15 '16 at 18:37
@Marco, I'd go further and say that this is something best done with the linear-algebraic route (that is, least squares), practically speaking. — J. M.'s missing motivation, Feb 15 '16 at 18:51
@MarcoB I'm actually trying to answer the question in general for people who may not have Mathematica (see linked post). I also believe that solving complicated linear equations (for 1000s of data points) may be more difficult (or at least not any easier) than having a closed form formula. In theory, we don't even need closed forms for linear regression, but we have those and consider them useful. — , Feb 15 '16 at 18:59

score 4 · Accepted Answer · edited Apr 13 '17 at 12:56

Here is my take at generating the identities you are trying to test; I will confess that I am not completely sure of what testing you need to carry out, so I hope that you will be able to compare the expressions obtained below with those you already have.

To set up the 3D linear regression problem I will use generic 3D points {x[i], y[i], z[i]}, and parameters $(a,b,c)$.

(* Generate the sum of squares to be minimized *)
Sum[Expand[(a x[i] + b y[i] + c - z[i])^2], {i, 1, n}]

sum of squares

(* Calculate the derivatives *)
Grad[%, {a, b, c}] // TableForm

gradient

(* Use linearity of sums *)
Distribute /@ % // TableForm

distributed form

At this point, you will want to pull out the numerical and parameter constants from the summations to simplify the problem. Below is a set of very handy replacement rules that will help you do that, courtesy of Peltio who originally used them with Integrate, but they work with Sum right out of the box after swapping the right function name in:

outrules = {
   Sum[f_ + g_, it : {x_Symbol, __}] :> Sum[f, it] + Sum[g, it],
   Sum[c_ f_, it : {x_Symbol, __}] :> c Sum[f, it] /; FreeQ[c, x],
   Sum[c_, it : {x_Symbol, __}] :> c Sum[1, it] /; FreeQ[c, x]
};

These must be applied repeatedly using ReplaceRepeated (//.) until the result doesn't change anymore:

(* Pull out any constants from summations *)
% //. outrules // TableForm

sum of squares in separated form

Now it's just a matter of setting the derivatives to zero to generate a system of three linear equations:

(* Set the derivatives equal to zero to generate the system of equations *)
Simplify[Thread[% == 0]] // TableForm

simplified equations

Now is a good time to simplify the notation a bit by introducing names for the summation results that act as constants in this system:

% //. {
   Sum[x[i], {i, 1, n}] -> sumX, Sum[y[i], {i, 1, n}] -> sumY, Sum[z[i], {i, 1, n}] -> sumZ,

   Sum[x[i]*y[i], {i, 1, n}] -> sumXY, 
   Sum[y[i]*z[i], {i, 1, n}] -> sumYZ, 
   Sum[x[i]*z[i], {i, 1, n}] -> sumXZ,

   Sum[x[i]^2, {i, 1, n}] -> sumX2, Sum[y[i]^2, {i, 1, n}] -> sumY2
 } // TableForm

simplified equations with named constants

Finally we can Solve this linear equation for $(a,b,c)$:

Solve[%, {a, b, c}]

explicit solutions

Thanks! As you point out, you're only solving 3 linear equations, and the number doesn't grow with n, the number of points. Other answers to similar questions on stats.stackexchange.com seem to suggest you end up with more equations as n grows, and you "need" linear algebra since there are so many equations. The fact that there are only 3 equations/3 unknowns allows for a simple closed-form solution. — , Feb 16 '16 at 13:00

Faster way to test possible points-to-plane-fitting identity?

1 Answers1

Linked