Move a point along a curve

Question

I am trying to implement the de Casteljau algorithm to trace a point along a Bézier curve.

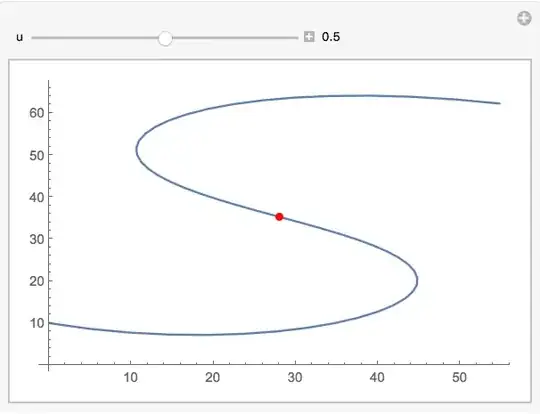
I already have the Bézier curve in place given by the control points

pts = {{54.78, 62.24}, {26.87, 68.24}, {1.58, 63.24}, 
       {-1, 49.18}, {1.58, 35.18}, {28.57, 35.03}, {52.41, 35.03}, 
       {60.48, 22.58}, {52.4, 7.4}, {24.27, 2}, {0, 10}};

I have been reading up on the de Casteljau algorithm and I understand the basic implementation of it, but I don't understand how to manipulate the point to move along the curve using the algorithm.

You might want to point to the textbook you're using so that answerers can write something you can easily relate to what you're reading. — J. M.'s missing motivation, Feb 16 '16 at 19:56
Do you really need to implement this algorithm on your own as opposed to simply using the built in BezierFunction ? — george2079, Feb 16 '16 at 20:03
Related: http://mathematica.stackexchange.com/questions/14736/how-to-draw-a-moving-point-on-a-curve — Michael E2, Feb 16 '16 at 23:59

score 5 · Answer 1 · edited Apr 13 '17 at 12:55

5

As suggested by george2079

pts = {{54.78, 62.24}, {26.87, 68.24}, {1.58, 63.24}, {-1, 49.18}, {1.58, 
    35.18}, {28.57, 35.03}, {52.41, 35.03}, {60.48, 22.58}, {52.4, 
    7.4}, {24.27, 2}, {0, 10}};

f = BezierFunction[pts];

llp = ListLinePlot[Table[f[t], {t, 0, 1, .02}]];

Manipulate[
 Show[llp,
  Epilog -> {Red, AbsolutePointSize[6],
    Point[f[u]]}],
 {{u, .5}, 0, 1, .01, Appearance -> "Labeled"}]

EDIT: In a comment, yode suggested the use of ParametricPlot). This has the advantage of exploiting the adaptive sampling of the built-in plotting functions and is more direct (i.e., you don't have to generate the Table of points used with ListLinePlot).

pp = ParametricPlot[f[t], {t, 0, 1}];

Manipulate[
 Show[pp,
  AspectRatio -> 1/GoldenRatio,
  Epilog -> {Red, AbsolutePointSize[6],
    Point[f[u]]}],
 {{u, .5}, 0, 1, .01, Appearance -> "Labeled"}]

edited Apr 13 '17 at 12:55

Community

1

answered Feb 16 '16 at 22:36

Bob Hanlon

157,611
7
77
198

f = BezierFunction[pts]; Manipulate[ Show[ParametricPlot[f[t], {t, 0, 1}], Epilog -> {Red, AbsolutePointSize[6], Point[f[u]]}], {{u, .5}, 0, 1, .01, Appearance -> "Labeled"}] – yode Feb 17 '16 at 16:39
@yode - Use of ParametricPlot is a good idea; however, since like the ListLinePlot it is independent of the Manipulate control, I would pull the plot outside of the Manipulate and use Show to keep the interaction as responsive as possible. Recommend that you post this as an answer. – Bob Hanlon Feb 17 '16 at 16:57
The honor should be attributed to you.I just wanna give a little advice to your answer. – yode Feb 17 '16 at 18:32
@yode - edited per your recommendation. – Bob Hanlon Feb 17 '16 at 19:15

Move a point along a curve

1 Answers1