1

My bifurcation diagram almost works, but I can't figure out how to replace the point number on the horizontal axis with the x coordinate from my calculation. I have tried a whole bunch of things that fail in various ways. The code is below. Help would be greatly appreciated.

bifurcation

z[0, c_] := c;
z[n_, c_] := z[n - 1, c]^2 + c;
zSeries[n_, len_, c_] := Module[{ser},
   ser = {z[n, c]};
   Do[AppendTo[ser, ser[[i]]^2 + c], {i, 1, len - 1}];
   ser];
ListPlot[Transpose[Table[zSeries[999, 100, x], {x, -2, .25, .0001}]], PlotStyle -> PointSize[Tiny]]

If I change the zSeries module to give each point its own x value, it gets VERY slow.

zSeries[n_, len_, c_] := Module[{ser},
   ser = {{c, z[n, c]}};
   Do[AppendTo[ser, {c, ser[[i]]^2 + c}], {i, 1, len - 1}];
   ser];
Jerry Guern
  • 4,602
  • 18
  • 47
  • Try the DataRange option in ListPlot. – bbgodfrey Feb 18 '16 at 01:41
  • 1
    Jerry, as bb says, you adjust DataRange so that the horizontal axis is in the right units. Look at the docs for it. BTW, NestList[] is pretty useful for implementing your zSeries. – J. M.'s missing motivation Feb 18 '16 at 02:05
  • 1
    Since the $x$-coordinate is fixed, you could just do something like {c, #} & /@ ser after generating them like in your original version. – J. M.'s missing motivation Feb 18 '16 at 02:41
  • @J.M. Yes, that's better coding, thank you. The lingering problem I have now is how much it slows down, but that might not be solvable. – Jerry Guern Feb 18 '16 at 02:45
  • 1
    Do you realize that Do[AppendTo[res, f[x]], {x, n}] is the same as res = Table[f[x], {x, n}], only 100 times slower (ignoring the time to compute f[x])? – Michael E2 Feb 18 '16 at 02:48
  • 2
    @Jerry, as I said, consider using NestList[]; repeated use of AppendTo[] is well-known to be a slow way of accumulating results. – J. M.'s missing motivation Feb 18 '16 at 02:50
  • @J.M. Ah! I was only using AppendTo[] because I didn't know about NestList[]. NestList[] does exactly what I wanted. Thank you. – Jerry Guern Feb 18 '16 at 04:04
  • This was a hugely helpful discussion. I had to learn 3 new Mathematica tricks to make this work, but I got it. I put all these helpful comments into the solution I posted as a second Answer. – Jerry Guern Feb 18 '16 at 05:05

2 Answers2

3

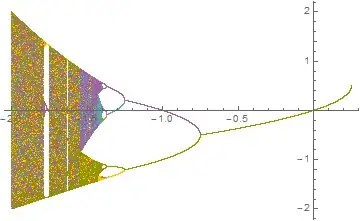
To illustrate my comment, is that what you had in mind?

ListPlot[Transpose[Table[zSeries[999, 100, x], {x, -2, .25, .0001}]], 
    PlotStyle -> PointSize[Tiny], DataRange -> {-2, .25}]

enter image description here

Addendum: Timing

The OP in his answer provides revised code,

z[0, c_] := c;
z[n_, c_] := z[n - 1, c]^2 + c;
ListPlot[Catenate[Table[{x, #} & /@ NestList[#^2 + x &, z[999, x], 100], 
    {x, -2, .25, .0001}]], PlotStyle -> PointSize[Tiny]]

which is much faster than the earlier code, requiring 64 sec (AbsoluteTiming) on my PC to generate the plot. Still, it seemed to me that further improvements in time could be achieved. Table requires 37 sec to generate the array, leaving 27 sec for ListPlot itself. Because as many as 100 duplicate points are plotted for x > -1.4, applying DeleteDuplicates offers an obvious savings. (It, like Catenate, takes negligible time.) Using FixedPointList instead of NestList also saves a bit of time for x > -.76, but only a few seconds, because the reduced list generation is largely offset by the test for a fixed point. Together, 

ListPlot[Catenate[Table[{x, #} & /@ DeleteDuplicates[
   FixedPointList[#^2 + x &, z[999, x], 100]], {x, -2, .25, .0001}]], 
   PlotStyle -> PointSize[Tiny], PlotRange -> All]

requires only about 41 sec. The other opportunity for savings involves replacing z[999, x], which takes some 31 sec in all, by the equivalent Nest[#^2 + x &, x, 999], 

ListPlot[Catenate[Table[{x, #} & /@ DeleteDuplicates[
    FixedPointList[#^2 + x &, Evaluate[Nest[#^2 + x &, x, 999]], 100]], 
    {x, -2, .25, .0001}]], PlotStyle -> PointSize[Tiny], PlotRange -> All]

which reduces total time to 11 sec, a significant improvement. (Using FixedPoint instead of Nest offers no further advantage.)

bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
  • It gets the job done in this case, because my x's happen to be evenly spaced. It's not really directly using my x coordinate. If my x's weren't evenly spaced, this wouldn't work. Does that make sense? – Jerry Guern Feb 18 '16 at 02:14
  • It's not the spacing being used here @Jerry; the horizontal axis is merely being scaled so that the left and right extents of the plot correspond to what's on your data. – J. M.'s missing motivation Feb 18 '16 at 02:16
  • I think I need to associate an x-value with each set of points calculated from that x. – Jerry Guern Feb 18 '16 at 02:17
  • @JerryGuern For non-uniformly spaced points, give ListPlot arrays of {x, y} values. (I see that you just suggested that yourself, and it should work.) I see no other way to plot randomly spaced points. – bbgodfrey Feb 18 '16 at 02:19
  • @bbgodfrey That was among the things I couldn't figure out how to make work. I have 100 y's associated with each x. – Jerry Guern Feb 18 '16 at 02:21
  • @JerryGuern Give each one its own x value. – bbgodfrey Feb 18 '16 at 02:22
  • @bbgodfrey I tried that just now and got it to work, but for some reason it is extremely slow. I put the code I used to add the x's in the Question. It works now, but the slowness is puzzling and displeasing. – Jerry Guern Feb 18 '16 at 02:35
  • @bbgodfrey Well anyway, you answered my question. Thank you! – Jerry Guern Feb 18 '16 at 02:45
  • I learned from this other Question that it was plotting slowly (and colorfully) because I had list-of-lists of pairs, and each list of pairs was getting styled differently. Using Catenate[] reduced the list-of-lists to a list. ListPlot[Catenate[Table[{x, #} & /@ NestList[#^2 + x &, z[999, x], 100], {x, -2, .25, .0001}]], PlotStyle -> PointSize[Tiny]] – Jerry Guern Feb 18 '16 at 10:00
  • 1
    @JerryGuern I have been able to reduce runtime by a factor of about six, as shown in the addition to my answer. Best wishes. – bbgodfrey Feb 18 '16 at 15:36
  • @bbgodfrey Thanks for follow-up. I've learned at least 5 new Mathematica commands from this discussion. I'm surprised that my recursive z[999,x] was so inefficient, but it looks like replacing that with Nest was the biggest speed gain. This has me thinking about other efficiencies now, since 999 and 100 are obviously just convenient large numbers. 999 lets the z[_,x] series get nearly asymptotic, and 100 is usually redundant but necessary at chaotic points. – Jerry Guern Feb 18 '16 at 20:26
  • 1
    @JerryGuern I too found this problem instructive. Your definition of z follows standard procedure, but in retrospect was consuming a lot of time. I shall consider that when I define similar functions. Cantenate was new to me, although it is not that different from Flatten. With my changes, the majority of the time now goes to ListPlot itself, so I think that the only way to save much more time is to plot fewer points. Best wishes. – bbgodfrey Feb 18 '16 at 23:11
2

From the OP: Based on the helpful Comments and Answer above, here's all I needed to do to get the plot I wanted:

z[0, c_] := c;
z[n_, c_] := z[n - 1, c]^2 + c;
ListPlot[Catenate[Table[{x, #} & /@ NestList[#^2 + x &, z[999, x], 100], {x, -2, .25, .0001}]], PlotStyle -> PointSize[Tiny]]
Jerry Guern
  • 4,602
  • 18
  • 47