Running out of PlotStyles for multiple curves within one graph in black and white

Question

This is related to the following thread "Plot curves different way so that one can see them when printing black and white"

But because my curves are close to each other in some regions, so just manipulating the "dotted" and "dashed" cannot clearly distinguish those curves in those regions. Changing thickness works better, but is not aesthetically pleasing.

I've seen the following cross-dotted style, can Mathematica replicate it? Or something similar such as strings of tiny squares or circles etc?

Answer 1

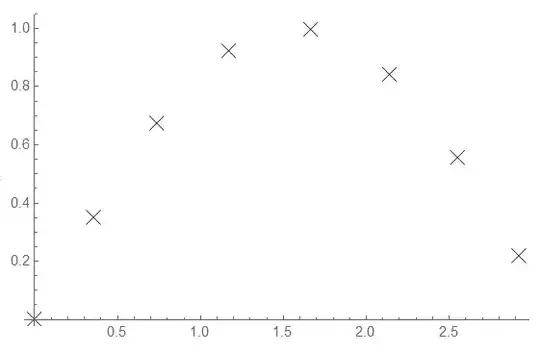
The way I do this is by using ListPlot witch has an option PlotMarkers. It can be anything:

 ListPlot[
    Table[Sin[x], {x, 0, Pi, 0.1}],
    PlotMarkers -> "x"
 ]

will yield this or even this:

ListPlot[
   Table[Sin[x], {x, 0, Pi, 0.1}],
   PlotMarkers -> (\!\(\*
      GraphicsBox[
      TagBox[PolygonBox[{{0, 0}, {1, 0}, {0, 1}}],
      "Triangle"],
      ImageSize->{13.999999999999815`, Automatic}]\))
]

with the following result

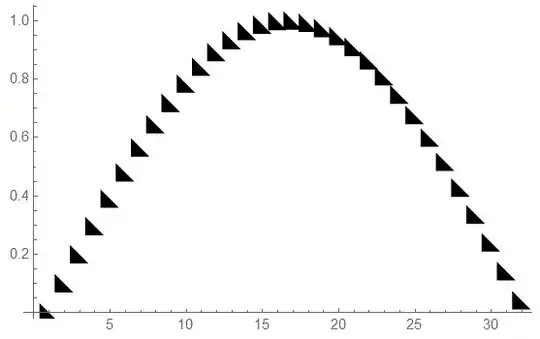
Have a look at the reference page PlotMarkers

EDIT

Saw the comment right before posting, but still here's how I would have done it:

SetAttributes[StepData, HoldAll];
StepData[fun_, xMin_, xMax_, dStep_] := Module[
   {xCur},
   xCur = xMin;
   res = Reap[
      While[xCur <= xMax,
       Sow[{xCur, fun[xCur]}];
       xCur += dx /. FindRoot[
          EuclideanDistance[{xCur, fun[xCur]}, {xCur + dx, fun[xCur + dx]}] == dStep,
          {dx, 0, 0, dStep}
          ];
       ]
      ][[2, 1]];
   Return[res];
   ];

func[x_] := Sin[x];
ListPlot[
 StepData[func, 0, Pi, 0.5],
 PlotMarkers -> {Graphics[
    {Black, Thin, Line[{{-0.1, -0.1}, {+0.1, +0.1}}], 
     Line[{{-0.1, +0.1}, {+0.1, -0.1}}]}
    ], 0.05}
 ]

With the following result