1

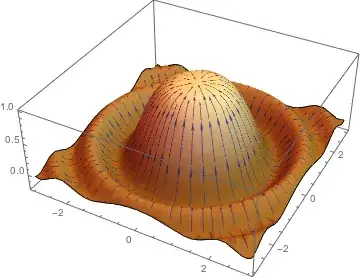
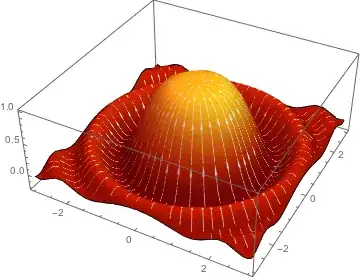
I want to plot a scalar-field $f(x,y) = \frac{sin(x^2+y^2)}{x^2+y^2}$ and it's gradient-field $\nabla f(x,y)$ in one graphic. Something like "StreamDensityPlot" in 3D. The mesh-lines on the scalar-field should look like arrows which are showing in the direction of the gradient. Thanks very much :)

astronerd
  • 21
  • 1

2 Answers2

4

Expanding on rewi's answer if you want the 3D result:

    f[x_, y_] := Sin[x^2 + y^2]/(x^2 + y^2)

    sdp =
     StreamDensityPlot[  Evaluate[{Grad[f[x, y], {x, y}], f[x, y]}], {x, -3,3}, {y, -3, 3},  PlotRangePadding -> 0, Frame -> False]

enter image description here

    Plot3D[f[x, y], {x, -3, 3}, {y, -3, 3}, PlotRange -> All, PlotStyle -> Texture[sdp], Mesh -> None]

enter image description here

Edit: Is there a bug with using StreamStyle with Texture? 

    sdp = StreamDensityPlot[
      Evaluate[{Grad[f[x, y], {x, y}], f[x, y]}], {x, -3, 3}, {y, -3, 3}, 
      PlotRangePadding -> 0, Frame -> False, 
      ColorFunction -> "SolarColors",
      StreamStyle -> White
    ]

enter image description here

The styling isn't carried over:?

    Plot3D[f[x, y], {x, -3, 3}, {y, -3, 3}, PlotRange -> All, 
     PlotStyle -> Texture[sdp], Mesh -> None]

enter image description here

But if we use StreamColorFunction:

    sdp = StreamDensityPlot[
      Evaluate[{Grad[f[x, y], {x, y}], f[x, y]}], {x, -3, 3}, {y, -3, 3}, 
      PlotRangePadding -> 0, Frame -> False, 
      ColorFunction -> "SolarColors",
      StreamColorFunction -> (GrayLevel[1] &)
    ]

enter image description here

    Plot3D[f[x, y], {x, -3, 3}, {y, -3, 3}, PlotRange -> All, 
     PlotStyle -> Texture[sdp], Mesh -> None]

enter image description here

Quantum_Oli
  • 7,964
  • 2
  • 21
  • 43
  • Thank you very much :) How can I change the colour of the scalarfield and the arrows ? – astronerd Feb 28 '16 at 11:36
  • If you look up StreamDensityPlot you'll find many options and examples of changing the various colors and stylings. You have to change them in the StreamDensityPlot, not the Plot3D as the former is used as a texture map for the later. I'll add an example to my answer. – Quantum_Oli Feb 28 '16 at 11:40
1

Is this what you are looking for?

f = Sin[x^2 + y^2]/(x^2 + y^2);
StreamDensityPlot[Evaluate[{Grad[f, {x, y}], f}], {x, -5, 5}, {y, -5, 5}]

enter image description here