How to use Scaled function

Question

I'm a beginner and I am really confused with the Scaled function:

What does 0.1, 0.2 mean?

Also, if I want to draw a 3d graph of $\frac{xy^2}{x^2+y^4}$, with 1, 2, 3, 5 marked on the x, y coordinate, what syntax should I use?

This is my code:

Show[{Plot3D[(x*y^2)/(x^2 + y^4), {x, -5, 5}, {y, -5, 5}, 
   AxesOrigin -> {0, 0, 0}, PlotRange -> {-1, 0.6}], 
  Graphics3D[{Text["x", Scaled[{-.05, .5, 0}], {0, -1}], 
    Text["y", Scaled[{.5, -.05, 0}], {0, -1}], 
    Text["z", Scaled[{.5, .5, 1.1}]]}]}, Boxed -> False]

It looks like the graph doesn't match when x,y is near 0, the limit should be 0.5. So I think I need to adjust the scaling.

Another problem is if x=0.01, y=0.1, the function's value should be 0.5, but (0.01,0.1,0.5) is not on the graph, is it still a problem about the scaling?

Something went wrong with your link; no image is showing. Please note also that it would be best for you to post your code in a copy / paste ready format, in addition to any images. — MarcoB, Feb 29 '16 at 00:52
I find this post confusing. Is the question about getting the ticks right or about scaling the x, y, and z axis labels. — m_goldberg, Feb 29 '16 at 02:01
The function does not have a unique limit at {0,0}. Mathematica fails to make a good plot because of this discontinuity. If you reduce the plot range to a much smaller region, you will find that the requested 0.5 value is somewhere there, but there will always be some nasty visual artifact near the origin. — LLlAMnYP, Feb 29 '16 at 13:13

score 3 · Answer 1 · edited Jun 16 '20 at 09:23

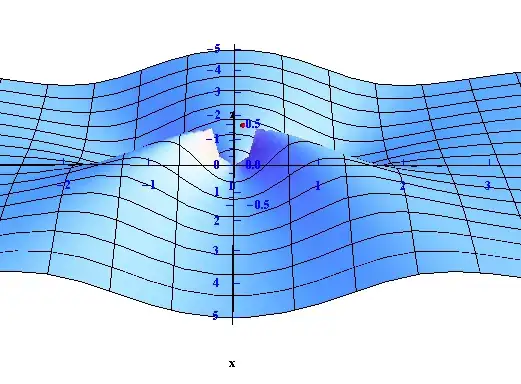
This will give you the ticks you appear to be requesting.

Show[
  {Plot3D[(x*y^2)/(x^2 + y^4), {x, -5, 5}, {y, -5, 5}, 
     AxesOrigin -> {0, 0, 0},
     BoxRatios -> {1.5, 1.5, 1},
     Mesh -> 5,
     Ticks -> {Range[-5, 5], Range[-5, 5], Automatic},
     TicksStyle -> Directive[Blue, Bold, 12]],
   Graphics3D[
     {Text[Style["x", Bold, 12], Scaled[{1.1, .5, .5}]],
      Text[Style["y", Bold, 12], Scaled[{.5, 1.1, .5}]],
      Text[Style["z", Bold, 12], Scaled[{.5, .5, 1.1}]]}]},
  Boxed -> False]

About the scaling I can't figure out what you are asking. I will note that

Limit[(x*y^2)/(x^2 + y^4), x -> 0]

0

not .5 as you seem to think.

Update

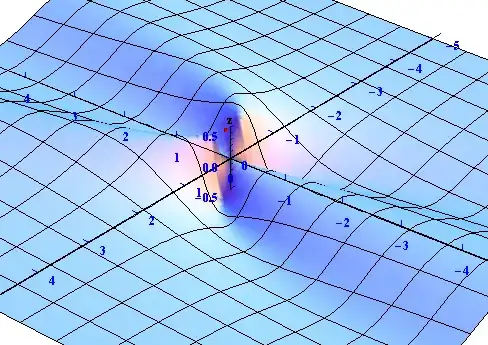
In a 3D plot the usual way to draw attention to a point is place a small sphere on the surface at the indicated xy-coordinates. This is also usually done with plots made with an undistorted Euclidean metric (BoxRatios -> Automatic) to keep the sphere to being distorted.

It is very hard to see the sphere unless it has a diameter of at least 1% of the maximum span of plot. This means the granularity of the visual point space is rather coarse.

Here is what adding such a sphere to your surface looks in an undistorted version.

f[x_, y_] := (x*y^2)/(x^2 + y^4)
Show[
  Plot3D[f[x, y], {x, -5, 5}, {y, -5, 5},
    AxesOrigin -> {0, 0, 0},
    PlotPoints -> 30,
    Ticks -> {Range[-5, 5], Range[-5, 5], Automatic}, 
    TicksStyle -> Directive[Blue, Bold, 12]],
  Graphics3D[
   {{Red, Sphere[{2., 3., f[2., 3.]}, Scaled[.0075]]},
    Text[Style["x", Bold, 12], Scaled[{1.1, .5, .5}]], 
    Text[Style["y", Bold, 12], Scaled[{.5, 1.1, .5}]], 
    Text[Style["z", Bold, 12], Scaled[{.5, .5, 1.1}]]}],
  BoxRatios -> Automatic,
  Boxed -> False]

I placed the point at {2, 3} so it us out in the open and easily seen. Note that I also converted the expression you are plotting into a function so the centers of any spheres you would wish to place on the surface can be readily calculated.

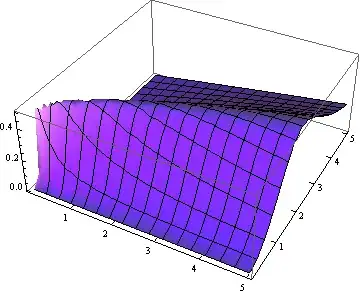
Update 2

The point {.01, .1, .5} is indeed on the surface. It is in a region where the surface is ill-behaved, so Mathematica has a hard time drawing there. In fact, when the domain is {x, -.5, .5}, {y, -.5, .5} Mathematica can't show what the region really looks like. To see that part of surface in detail, the domain must be greatly restricted. Even then Mathematica has to work hard.

Here a plot that shows the section you are interested in sufficient detail:

Show[
  Plot3D[f[x, y], {x, -.5, .5}, {y, -.5, .5},
    AxesOrigin -> {0, 0, 0},
    MaxRecursion -> 5,
    PlotPoints -> 200], 
  Graphics3D[{Red, Sphere[{.01, .1, f[.01, .1]}, Scaled[.0075]]}], 
  BoxRatios -> Automatic,
  Boxed -> False]

Note how the red dot is sitting on a razor sharp ridge, just a bit off from a what appears to be a deep plunge to zero. However, the plunge is an artifact of the plotting process. The ridge actually runs across the x = 0 line, but the inflection becomes so sharp, Mathematica can't show it.

The topography of the region around {.01, .1} makes it hard to plot.

Thanks for your answer. I also want to spot a point on the graph for example when x=0.01, y=0.1, and I want to mark the point in red on the graph, what's the syntax for it — whoisit, Feb 29 '16 at 05:58
@whoisit. At the scale of this plot, a point at {.01, .1} can't be distinguished from a point at {0, 0}. — m_goldberg, Feb 29 '16 at 06:15
Thanks again for your answer. I still don't get it that if I set x=0.01, y=0.1, the function's value is 0.5, but (0.01,0.1,0.5) is not on the graph? I have added new pictures in my original post, It is a red dot that repesents (0.01,0.1,0.5), it's obvious not on the graph — whoisit, Feb 29 '16 at 08:28

score 2 · Answer 2 · answered Feb 29 '16 at 00:50

2

Plot3D[x y^2/(x^2 + y^4), {x, 0, 5}, {y, 0, 5}, 
       Ticks -> {Range@5,Range@5}]

Mathematica graphics

answered Feb 29 '16 at 00:50

Dr. belisarius

115,881
13
203
453

Thanks for your answer. I also want to spot a point on the graph for example when x=0.01, y=0.1, and I want to mark the point in red on the graph, what's the syntax for it – whoisit Feb 29 '16 at 02:12
2

@whoisit Strongly related to your comment: http://meta.mathematica.stackexchange.com/q/1808/193 – Dr. belisarius Feb 29 '16 at 02:14
1

Nice link, particularly the third comment. – rhermans Feb 29 '16 at 08:30

How to use Scaled function

2 Answers2

Update

Update 2

Linked