I've defined a set of rules, which I want to use with FullSimplify, as follows:
transf1[expr_] := expr /. (a_⊕b_)⊕c_ -> a⊕(b⊕c)
transf2[expr_] := expr /. a_⊕b_ -> b⊕a
transf3[expr_] := expr /. a_⊕-a_ -> 0
transf4[expr_] := expr /. a_⊕0 -> a
transf5[expr_] := expr /. a_⊖b_ -> a⊕-b
But when I try to actually use them, I get no result:
FullSimplify[x⊕y⊖x,TransformationFunctions->{transf1,transf2,transf3,transf4,transf5}]
x⊕(y⊖x)
At the same time, there does exist a sequence of transformations, which does yield a simpler result:
transf4@transf3[transf2 /@ transf1@transf2@transf5[x⊕y⊖x]]
y
Am I using FullSimplify wrongly? Isn't the above the correct way to provide custom transformation functions?
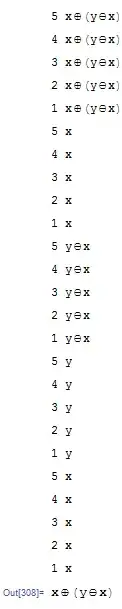

FullSimplifywon't evaluate all possible compositions.... perhaps a modifiedComplexityFunctionis necessary to guide it through a good path – Dr. belisarius Feb 29 '16 at 21:00