Do[ ]s and Don't[ ]s when teaching Mathematica in undergraduate courses

Question

Question motivated by some horrific homework-related posts that I don't dare to link:

What are the top Do's and Dont's when teaching Mathematica to undergrads?

I don't ask for the design of a curriculum, but just the most relevant points to be aware of, written in a way that could benefit present and future teachers

Please be aware that this question isn't about how you should program in Mathematica, but about how and what and in what order you should teach it to a specific audience.

I'm not sure Don't[] is syntactically proper. :D Less facetiously, wouldn't this have some overlap with the pitfall thread? — J. M.'s missing motivation, Mar 03 '16 at 15:32
Isn't this just another version of the pitfalls question? Is this substantially different from that one? — rm -rf, Mar 03 '16 at 15:33
Also, I wouldn't be too quick to denigrate Do[]; loops have their place, too. — J. M.'s missing motivation, Mar 03 '16 at 15:34
@R.M., who the hell multiplies with a naked Derivative[]? ;P — J. M.'s missing motivation, Mar 03 '16 at 15:35
@J.M. "Start by teaching how to manage lists". is a valid point here that doesn't fit well on the pitfalls q — Dr. belisarius, Mar 03 '16 at 15:37
In that case, can you find time to expand on that, at least so this one's made to be clearly distinct? — J. M.'s missing motivation, Mar 03 '16 at 15:41
I've seen a large number of courses taught with Mathematica. Helped debug code in many of them. I even took one when an undergrad. I could write for days. My advice is very similar to advice for good programming in general. (1) Make many small notebooks instead of a few large notebooks. (2) Limit global state and global values. (3) Use descriptive variable names. — Searke, Mar 03 '16 at 15:46
The activities in the notebook should be more than "read this then evaluate these cells". It's easy to fall into this trap. The first time you write content, it will look like this. If, for example, you have a manipulate, ask the student something like "for what values does x happen?" and then ask them to take a snapshot of the manipulate. Just because you've added a manipulate to some text doesn't mean you've made an interactive or engaging course. — Searke, Mar 03 '16 at 15:48
"Just because you've added a Manipulate to some text doesn't mean you've made an interactive or engaging course." - that sounds like an answer, @Searke… :) — J. M.'s missing motivation, Mar 03 '16 at 15:58
@J.M. You know, I'm the rebellious type. A high voted answer here could be a tool to exert some pressure on FORTRAN lovers teaching Mathematica. — Dr. belisarius, Mar 03 '16 at 16:03
Add this in the init.m before starting to learn: Unprotect /@ {For, While}; For = While = Nothing; Protect /@ {For, While}; :D — rm -rf, Mar 03 '16 at 16:14
I do like that it's relatively easy to tell from the code if the writer was a refugee from FORTRAN-ville… :D — J. M.'s missing motivation, Mar 03 '16 at 16:16
It seems that any reasonable answer will have significant overlap with the following questions: Is it necessary to have a prior computational background or is it possible to learn Mathematica as a first programming language?, and depending on the goal of the course: Having used Mathematica as a “gateway” language, where to from here?. There is also a difference between using and teaching Mathematica in class. Seems you 're talking more about using... — Jens, Mar 03 '16 at 17:12
@Jens I was trying to refer to teaching Mathematica. And the answers I expect should "talk" to teachers. Please give me some advice on how do you think I could clarify it — Dr. belisarius, Mar 03 '16 at 17:37
@Dr.belisarius Ah, so would it be OK if the answer included "teaching programming" as part of teaching Mathematica? Because I think it's wrong to see Mathematica as an extension of a calculator, or table of integrals, or even spreadsheet (although those are "use cases"). Programming has to be part of it. — Jens, Mar 03 '16 at 18:17
@Jens Agree, like in "Programming", but not like in "Computer Science" — Dr. belisarius, Mar 03 '16 at 18:19
Victoria (the state not the queen) has had a statewide Mma license in schools for 3 years. The authorities have trialed computer based final year math exam for the past 3 years. Not sure how the teacher go about teaching Mma. To deploy Mma for computer based assessment one of the conditions was that the notebook had to be typeset identical to the printed exam (which comes back to the typsetting issue). Also student undertake trial Mma based exams prior to their final. On exam day they use their laptops for the Mma based final exam. This is not an answer but peripherally of interest?? — Mike Honeychurch, Mar 03 '16 at 21:52
@MikeHoneychurch Although it isn't what I had in mind when asking the question, I believe that other Victorias (states, not queens) may benefit from having the full info about the "experiment" available — Dr. belisarius, Mar 03 '16 at 23:21
@Dr.belisarius okay I'll post some more details either later today or tomorrow — Mike Honeychurch, Mar 04 '16 at 01:47

score 13 · Answer 1 · edited Jun 16 '20 at 09:23

Draft - writing took longer than I thought, and I'm late for class...

I've given this question a lot of thought, and while I'm not overly convinced that my reflections are useful to a wide audience, they might be insightful to some. (At the very least, it provides me with a rationale to sit and organize my own thoughts.)

Know your pedagogy

Learning outcomes: While there are courses intended to teach a particular programming language, I suspect more often than not, a programming language is taught within the context of another subject. That is certainly the case for me, trying to introduce Chemistry majors to the benefits of using Mathematica in their data analysis.
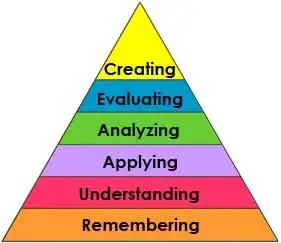
Learning domains: Spending time "learning about learning" has helped (me) greatly in developing successful lessons. I am a fan of Bloom's Taxonomy which is a tool for categorizing educational goals (and therefore is closely associated with the previous bullet). It helps me develop a strategy for creating an effective lesson or activity by providing "bins" for the various elements of a lesson. I can look at the lesson and ask "what am I asking the students to apply?" or "am I over-emphasizing remembering of facts?"

Understand your students' perspective: Lastly (for now) is that you should consider your students' academic history. My students have virtually no programming knowledge or experience. Naturally, there are disadvantages (how much programming do I teach in an instrumental methods class) and advantages (they have no idea what a for/while loop is, so I won't have to tell them not to use it).

From pedagogy to practice

Much of what I need students to do can be summed up in the 'motto' "Mathematica can do it better than Excel ... most of the time". An example set of learning outcomes for the statistics portion of an upper-level instrumental methods class might be

Upon completing this course, most students can

use linear regression statistics to evaluate the quality of an instrument response in relationship to substrate concentration;
estimate how measurement errors are propagated through to the desired result;
utilize the student's t-test to determine whether or not the differences in two sets of measurements are statistically significant.

For the first point, I spend much time on how Excel's linest() function provides the necessary information. LinearModelFit naturally provides all of this information as well; however, I feel that students have a better chance of being exposed to Excel in the workforce than Mathematica, which adds more value to the Excel skill.

I have had more success with incorporating Mathematica into the error propagation activities. My students, sadly, have weak mathematical backgrounds and calculus is not their strong suit. Nonetheless, having a platform that allows students to perform partial differentials confidently (even if they don't - but should - know how the answer is obtained) allows me to incorporate higher-order elements of Bloom's taxonomy into my lessons (e.g. instead of remembering a separate formula for addition and multiplication of measurements with errors, they learn to apply a a single equation applicable to both situations).

Practical considerations

Perhaps the real answer to the question asked is here. Students in the chemical sciences need these Mathematica basic skills

Import data (typically in CSV format)
List manipulation as it pertains to filtering out nested lists and removing rows and columns that contain non-numeric information
Plot of discrete data AND formatting of the plot to display axes labels and other information typically expected of a publication-quality plot
Descriptive statistics, linear regression and t-test
Occasionally, curve integration (determining peak area of an imported spectrum)

I have had success with creating CDFs and Notebooks that minimize student exposure to the underlying Wolfram Language stuff. While I feel somewhat guilty about the black-box nature of the activities (especially since I'm teaching upper level courses designed to get students thinking about what's in the black box), I fall back to the learning outcomes for my course, which at the end of the day are not programming focused.

One caveat is to make efforts NOT to turn your CDFs/notebooks into show-off eye-candy displays. We all know that Mathematica is very powerful, and with a few obfuscated lines of code one can create some pretty powerful results. The point is not to "wow" students with your skills, but to provide them with tools to develop their own skills.

The most important step

I've had the best success in incorporating Mathematica into my instruction when I have taken the time to reflect on student performance. Assessing student performance (i.e. assigning a grade) is only the first step in the reflection process. Determining whether or not the students achieved the learning outcomes, identifying the current roadblocks and revising your curriculum in response to these findings complete the process and will ultimately result in improved student performance over the long run.

Nice answer! Blackboxing is a "two-edged blade", but most interesting Mma functions are exactly that, anyway :). — Dr. belisarius, Mar 03 '16 at 18:13
BTW: Do you suggest your students to use this site? If yes: For what? — Dr. belisarius, Mar 03 '16 at 18:17
@Dr.belisarius I encourage my research students (undergraduates) to use the site, but not the general lecture/lab students. The research students are sufficiently engaged in Mathematica programming that they will take the time to look at the documentation first before asking questions. Your question does bring up an interesting point on how to teach my lecture/lab students to effectively obtain guidance from the body of questions that are already present on the site. Must do some more reflecting.... — bobthechemist, Mar 04 '16 at 00:06
I asked because I think there are several ways to use the site. All the SE infrastructure is focused on providing ways to find answers to specific problems, but nevertheless a student may focus on a topic (let's say compiling, feature recognition, Diophantine problems, whatever) and get a lot of useful guidelines to learn about it. — Dr. belisarius, Mar 04 '16 at 03:01

Mike Honeychurch · Answer 2 · 2016-03-04T04:46:29.933

In Victoria the state education department has been trialing computer based assessment as a replacement for paper exams for the final year of high school math method exam. The computer based assessment is written in Mathematica.

Some considerations:

Mathematica is used in the curriculum although I am not sure to what extent. I think it probably depends on the teachers proficiency but generally the schools involved in the trial have teachers are are confident with Mathematica.

Students are given trial exams in the lead up to the final so that they are familiar with the computer based format (it is assumed on exam day that they have sufficient Mathematica knowledge to be able to complete the exam).

The exam is typeset by an agency within the education department. Because of security issues it is not subcontracted. To assist with the production of the exam they have a production palette.

The exam is available for download on exam day by secure FTP. The schools' technicians get the download and install the exam on student laptops via an installer.

The exam notebook mimics the printed paper exam. It comprises 20 multiple choice questions followed by several other questions that contain parts and sub-parts. These questions typically contain equation and plots and require the student to write and evaluate code to generate an answer to the question.

A lot of Mathematica menu functionality is suspended during the exam. The only means of student input are by clicking radio button multiple choice and input cells and text cells (for additional explanation of an answer).

Mathematica is locked (selectable -> false etc) during the reading time. Reading time and exam time are set as scheduled tasks but can be overridden by staff in special circumstances.

At the conclusion of the exam the notebooks are collect by the school technician and securely sent back to the department.

A multiple choice question:

A detailed question:

Here is an example of creating some multiple choice stuff:

About instrumentation: Preparing the whole environment in Mma looks like a decent size task (to say the least). What kind of profiles are involved?. For example:are there non-sci programmers who learned Mma just to make this happen? — Dr. belisarius, Mar 04 '16 at 03:32
That part you covered ("The exam is typeset by an agency within the education department."). I meant developing the template, securing the transfers and the notebooks, developing the runtime environment for the exams, collecting and graduating the exams, etc — Dr. belisarius, Mar 04 '16 at 03:59
@Dr.belisarius there is an agency with the acronym VCAA that oversees all exams. they develop the exam notebook using a palette I made them. Collecting the exams and sending them back is done by schools for final year exams anyway so the only difference is they are collecting notebooks on a USB and FTPing back rather than collecting exam papers and courier them back. Similarly the grading has to occur for all exams statewide anyway. The multiple choice is marked automatically and the other questions in the notebook are marked the same as if in an exam paper — Mike Honeychurch, Mar 04 '16 at 04:42
...so the infrastructure is already in place because all students sit a final exam for each subject at high school and the exams for all subjects are set, monitored and marked by the VCAA. — Mike Honeychurch, Mar 04 '16 at 04:43
Thanks a lot for the explanation. Easier than it looked at first ... and you were there :) — Dr. belisarius, Mar 04 '16 at 06:01

Do[ ]s and Don't[ ]s when teaching Mathematica in undergraduate courses

2 Answers2

Know your pedagogy

From pedagogy to practice

Practical considerations

The most important step