Fitting Coxian distribution to some data

Question

I'm trying to fit a transformed (actually shifted to the right) Coxian distribution to some data ( if needed an example set is here Sim data ). I've tried a number of ways for this:

1. FindDistributionParameters in my case yields the worst results.
2. FindFit to fit the PDF of the distribution to a HistogramList works the best atm
3. NMinimize the distance between the distribution moments to data moments

I as well tried to combine those methods by providing the starting values (and here random starting values work a little bit better than some meaningfull values obtained via FindInstance).

My question is how to enchance my solutions and why some of them do not work like others?

Here's something I tried: (Off-topic question - how can I hide some part of the post for it not to be long?)

---

The first approach is with direct FindDistributionParameters

simData = 
  Import["fitData.txt", "Table"];

phasesToUse = 3;
distrShift = 10;
distrStart = 0;

Clear[coxModel];
coxModel[p_] := coxModel[p] = TransformedDistribution[
    x + distrShift,
    x \[Distributed] CoxianDistribution[
      Table[\[Alpha][j], {j, 1, p - 1}],
      Table[\[Lambda][j], {j, 1, p}]
      ]
    ];
Clear[coxModelPDF];
coxModelPDF[p_] := coxModelPDF[p] = PDF[
    coxModel[p],
    x
    ];

resFindParam = FindDistributionParameters[
   simData,
   coxModel[phasesToUse]
   ];

resFindParam
Show[{
  Histogram[simData, {0.5}, "PDF"],
  Plot[
   (*Evaluate[*)coxModelPDF[x](*]*),
   {x, distrShift, 30}
   ]
  }]

As you can see, FindDistributionParameters failed horribly here. Think it found some local minimum and failed to find anything better.

---

Next I tried to supply an initial guess by finding a point that fits the first moment of data:

initVals = FindInstance[
     Evaluate[And @@ Join[
        {0.9 <= Moment[coxModel[phasesToUse], 1]/
          Moment[simData[[All, pointToApprox]], 1] <= 1.1},
        {coxModelPDF[phasesToUse, distrShift] == distrStart},
        Table[0 <= \[Alpha][i] <= 1, {i, 1, phasesToUse - 1}],
        Table[\[Lambda][i] >= 0, {i, 1, phasesToUse}]
        ]],
     Join[
      Table[\[Alpha][i], {i, 1, phasesToUse - 1}],
      Table[\[Lambda][i], {i, 1, phasesToUse}]
      ]
     ][[1]] /. {\[Alpha] -> \[Alpha]I, \[Lambda] -> \[Lambda]I};
resFindParam = FindDistributionParameters[
   simData[[All, pointToApprox]],
   coxModel[phasesToUse],
   Join[
     Table[{\[Alpha][i], \[Alpha]I[i]}, {i, 1, phasesToUse - 1}],
     Table[{\[Lambda][i], \[Lambda]I[i]}, {i, 1, phasesToUse}]
     ] /. initVals
   ];

Unfo, in this case it repeats the previous case or just almost infinitely tries to find parameters.

---

Then I tried to NMinimize the distance between at least the first two moments and then to feed it to FindDistributionParameters:

simData = 
  Import["fitData.txt", "Table"];

momentsToMin = 2;
phasesToUse = 3;
distrShift = 10;

Clear[simMoment];
simMoment[n_, i_] := simMoment[n, i] = Moment[
    simData,
    i
    ];

Clear[coxMoment];
coxMoment[p_, i_] := coxMoment[p, i] = Moment[
    TransformedDistribution[
     x + distrShift,
     x \[Distributed] CoxianDistribution[
       Table[\[Alpha]T[i, j], {j, 1, p - 1}],
       Table[\[Lambda]T[i, j], {j, 1, p}]
       ]
     ],
    i
    ];

tmpEnum = 0;
minRes = NMinimize[
   {
    Evaluate[Plus @@ Table[
       SquaredEuclideanDistance[
        Join[Table[\[Alpha][i], {i, 1, phasesToUse - 1}], 
         Table[\[Lambda][i], {i, 1, phasesToUse}]],
        Join[Table[\[Alpha]T[k, j], {j, 1, phasesToUse - 1}], 
         Table[\[Lambda]T[k, j], {j, 1, phasesToUse}]]
        ],
       {k, 1, momentsToMin}
       ]],
    Evaluate[And @@ Join[
       {PDF[
          TransformedDistribution[
           x + distrShift,
           x \[Distributed] CoxianDistribution[
             Table[\[Alpha][i], {i, 1, phasesToUse - 1}],
             Table[\[Lambda][i], {i, 1, phasesToUse}]
             ]
           ],
          distrShift
          ] == 0},
       Table[
        coxMoment[phasesToUse, k] == simMoment[pointToApprox, k],
        {k, 1, momentsToMin}
        ],
       Table[0 < \[Alpha][i] < 1, {i, 1, phasesToUse - 1}],
       Table[\[Lambda][i] > 0.01, {i, 1, phasesToUse}],
       Flatten[
        Table[0 < \[Alpha]T[k, j] < 1, {j, 1, phasesToUse - 1}, {k, 1,
           momentsToMin}]],
       Flatten[
        Table[\[Lambda]T[k, j] > 0.01, {j, 1, phasesToUse}, {k, 1, 
          momentsToMin}]]
       ]]
    },
   Join[
    Table[\[Alpha][i], {i, 1, phasesToUse - 1}],
    Table[\[Lambda][i], {i, 1, phasesToUse}],
    Flatten[
     Table[\[Alpha]T[k, j], {j, 1, phasesToUse - 1}, {k, 1, 
       momentsToMin}]],
    Flatten[
     Table[\[Lambda]T[k, j], {j, 1, phasesToUse}, {k, 1, 
       momentsToMin}]]
    ],
   EvaluationMonitor :> (tmpEnum++; 
     If[Mod[tmpEnum, 200] == 0, Print[tmpEnum];];)
   ];

distrRes = FindDistributionParameters[
   simData,
   TransformedDistribution[
    x + distrShift,
    x \[Distributed] CoxianDistribution[
      Table[\[Alpha]F[i], {i, 1, phasesToUse - 1}],
      Table[\[Lambda]F[i], {i, 1, phasesToUse}]
      ]
    ],
   Join[Table[{\[Alpha]F[i], \[Alpha][i]}, {i, 1, phasesToUse - 1}], 
     Table[{\[Lambda]F[i], \[Lambda][i]}, {i, 1, phasesToUse}]] /. 
    minRes[[2]]
   ];

minRes
distrRes
Show[{
  Histogram[simData, {0.5}, "PDF"],
  Plot[
   Evaluate[PDF[
     TransformedDistribution[
       x + distrShift,
       x \[Distributed] CoxianDistribution[
         Table[\[Alpha][i], {i, 1, phasesToUse - 1}],
         Table[\[Lambda][i], {i, 1, phasesToUse}]
         ]
       ] /. minRes[[2]],
     x
     ]],
   {x, distrShift, 30}
   ],
  Plot[
   Evaluate[PDF[
     TransformedDistribution[
       x + distrShift,
       x \[Distributed] CoxianDistribution[
         Table[\[Alpha]F[i], {i, 1, phasesToUse - 1}],
         Table[\[Lambda]F[i], {i, 1, phasesToUse}]
         ]
       ] /. distrRes,
     x
     ]],
   {x, distrShift, 30},
   PlotStyle -> Red
   ]
  }]

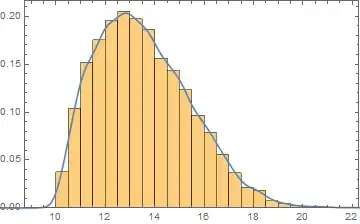
The result is:

Where the blue line is for the parameters after NMinimize and the red is for FindDistributionParameters after that. This is better now, but still not the best thing. Yet it is possible to obtain better results.

---

The last thing I tried is to directly fit the PDF to the HistogramList

simData = 
  Import["fitData.txt", "Table"];

phasesToUse = 3;
distrShift = 10;
distrStart = 0;

histStep = 0.5;

tmpFitData = 
  HistogramList[simData, {histStep}, "PDF"];
fitData = 
  Join[{{tmpFitData[[1, 1]], 0}}, 
   Table[{(tmpFitData[[1, i + 1]] + tmpFitData[[1, i]])/2, 
     tmpFitData[[2, i]]}, {i, 1, Length[tmpFitData[[2]]]}]];

Clear[coxModel];
coxModel[p_] := coxModel[p] = TransformedDistribution[
    x + distrShift,
    x \[Distributed] CoxianDistribution[
      Table[\[Alpha][j], {j, 1, p - 1}],
      Table[\[Lambda][j], {j, 1, p}]
      ]
    ];
Clear[coxModelPDF];
coxModelPDF[p_, x_] := coxModelPDF[p, x] = PDF[
    coxModel[p],
    x
    ];

fitPars = FindFit[
   fitData,
   {
    coxModelPDF[phasesToUse, x],
    Evaluate[And @@ Join[
       {coxModelPDF[phasesToUse, distrShift] == distrStart},
       Table[0 < \[Alpha][i] < 1, {i, 1, phasesToUse - 1}],
       Table[\[Lambda][i] > 0.01, {i, 1, phasesToUse}](*,
       Flatten[Table[(\[Lambda][i]/\[Lambda][
       j]\[LessEqual]0.95||\[Lambda][i]/\[Lambda][
       j]\[GreaterEqual]1.05),{i,1,phasesToUse},{j,i+1,
       phasesToUse}]]*)
       ]]
    },
   Join[
    Table[\[Alpha][i], {i, 1, phasesToUse - 1}],
    Table[\[Lambda][i], {i, 1, phasesToUse}]
    ],
   x(*,
   MaxIterations\[Rule]1000*),
   Method -> NMinimize(*,
   NormFunction\[Rule](Norm[#, 2] & )*)
   ];

fitPars
Show[{
  Histogram[simData, {0.5}, "PDF"],
  Plot[
   Evaluate[coxModelPDF[phasesToUse, x] /. fitPars],
   {x, distrShift, 30}
   ]
  }]

Result:

This is the best I could obtain till now. But I'm sure that there is a way to find a better fit and/or improve my codes.

Any feedback is welcome and sorry for the long post.

Answer 1

Not an answer ... more a comment that is too long for the comment box. I found your question difficult to follow, mainly because it sets up lots of functions and models and this and that ... and all we really need to know -- which is not shown -- is what is the functional form of the pdf that you are actually using. And that appears to be:

p = 3;
PDF[TransformedDistribution[x + 10, x \[Distributed] 
CoxianDistribution[Table[\[Alpha][j], {j, 1, p - 1}], 
 Table[\[Lambda][j], {j, 1, p}]]], x] // Simplify

... which produces this output for the pdf:

_{(source: tri.org.au)}

... which is a model requiring that you estimate 5 separate parameters.

In summary:

• you have a fairly simple, almost elementary shaped empirical pdf (your histogram) ... which one should be able to easily capture beautifully with a 1 or 2 parameter distribution ... and

• instead, you are trying to model it with a distribution that requires 5 parameters. Presumably you have some good solid foundation for using the Coxian model (????), but when it comes to estimation: less is more.

To illustrate the point neatly, here is a single parameter fit to your data using a Rayleigh distribution with pdf:

$$f(x) = \frac{x}{s^2} \exp \left(-\frac{x^2}{2 s^2}\right) \quad \text{ for } x > 0 $$

 sol = FindDistributionParameters[simData-10, RayleighDistribution[s]]

{s -> 2.84301}

And here is the fit ... which is far better, with just a 1 parameter model than the 5 parameter Coxian:

_{(source: tri.org.au)}

Answer 2

This answer uses multiple Coxian distributions to approximate the PDF for the data given in the question, SimData. It is in the same spirit as of my answers to "Findfit does not find the best fit" and "Non-linear curve fit problem".

I think the answer fits the question request for

"[...] how to enchance my solutions and why some of them do not work like others?"

Using multiple Coxian PDF's is an enhancement, and the resutls probably explain why it is not easy to find good approximations using fittings of one Coxian PDF.

Also, examining a fitted sum of Coxian PDF's that gives a good approximation can help selecting the parameters for a single Coxian PDF if that is desired.

Procedure outline

1. Generate a basis of many (e.g. 20,000 or 100,000) Coxian PDF functions over a Cartesian product of parameter ranges. The parameter ranges are selected to be close to the observed distribution.

2. From the data make a set of PDF approximate estimates using large enough samples. (E.g. 10 or 30 sets of based on 2000 points each.) This is to help the next step.

3. Find a linear fit of the Coaxian PDF functions from step 1 to the points from step 2.

4. Verify the obtained result.

I did the fit using my QuantileRegression package because using LinearModelFit was too slow and I was getting over-fitted results.

Code

0. Load the data

simData = Flatten@ Import["https://dl.dropboxusercontent.com/u/315629/StackExchange/fitData.txt", "Table"];
simData = Transpose[{Range[Length[simData]], Flatten@simData}];

1. Generating a basis of many Coxian PDF functions (20,000 to 100,000):

pfuncs = Table[
   Piecewise[{{(\[Alpha]*\[Lambda]1*\[Lambda]2)/(E^(\[Lambda]2*(x - \
\[Mu]))*(\[Lambda]1 - \[Lambda]2)) + (\[Lambda]1*(1 - \[Alpha] + (\
\[Alpha]*\[Lambda]2)/(-\[Lambda]1 + \[Lambda]2)))/
              E^(\[Lambda]1*(x - \[Mu])), x - \[Mu] >= 0}}, 
    0], {\[Mu], 10.2, 12, 0.2}, {\[Alpha], 0, 1, 0.1}, {\[Lambda]1, 
    0.01, 3.5, 0.25}, {\[Lambda]2, 0.02, 13, 0.2}];
pfuncs = Union[Flatten[pfuncs]];
Length[pfuncs]

(* 91140 *)

Here is a sample of these basis functions:

2. Make "a dozen" (from 10 to 100) PDF approximations:

xMultPDFPairs = Table[(
    hl = HistogramList[RandomSample[simData[[All, 2]], 4000], 30, "PDF"]; 
    N@Transpose[{Mean /@ Partition[hl[[1]], 2, 1], hl[[2]]}]), {10}];

3. Fit the Coaxian PDF's to the PDF approximations:

Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/QuantileRegression.m"]

AbsoluteTiming[
 qXPDFInt = 
  QuantileRegressionFit[Join @@ xMultPDFPairs, pfuncs, x, {0.5}, 
    Method -> {LinearProgramming, Method -> "CLP"}][[1]]
 ]

qXPDFInt = Simplify[qXPDFInt];
qXPDFInt = Function[Evaluate[qXPDFInt /. {x -> #}]]

3.1. This plots the PDF approximations points and the fitted Coxian linear model:

xps = Join @@ xMultPDFPairs;
Show[{ListLinePlot[{#, qXPDFInt[#]} & /@ Union[Sort[xps[[All, 1]]]], 
   PlotStyle -> Pink, PlotRange -> All], ListPlot[xps]}]

4. Verification with plots:

Show[{
  Histogram[simData[[All, 2]], 40, "PDF"],
  ListLinePlot[{#, qXPDFInt[#]} & /@ Union[Sort[xps[[All, 1]]]], 
   PlotStyle -> Red, PlotRange -> All]}]

Using B-splines over CDF's

Before coming up with the answer above I used B-splines fitted over CDF approximate estimates. The resulting PDF was derived by differentiating the obtained B-spline CDF. Here is an example:

Answer 3

When one has a large sample from a continuous probability distribution as you do, one does not always need to be restricted to methods of fitting a specific distribution with a parsimonious number of parameters.

Yes, when you know the form of the distribution and just have to estimate a few parameters, that's great. But if you don't have to compare specified parameters among data sets and just need to estimate the probability density function (and any summaries based on the probability density function), using nonparametric density estimation can be just what you need.

For example, if you're a Bayesian and don't (or can't) know the form of the posterior distribution, what's the next best thing? A very large sample from that posterior distribution.

Mathematica has the function SmoothKernelDistribution from which you can obtain estimates of the mean, variance, percentiles, probability density function (at any point), cumulative distribution function, etc. Such summary statistics might be better things to compare among different data sets than parameters from a specific form of probability density function. And you have the luxury of a large sample size (12,000 for your posted example).

Here are the commands that could be used:

kde = SmoothKernelDistribution[simData];
Show[Histogram[simData, "Knuth", "PDF", PlotRange -> {{9, 22}, Automatic}, Frame -> True], 
 Plot[PDF[kde, t], {t, 0, 1.1 Max[simData]}]]

Answer 4

As @wolfies states you should likely consider simpler models to describe (as opposed to "explain") your data. However, if you do need to use the Coxian distribution, then you might consider calculating AIC values for small values of p to help determine which value of p works best (with respect to AIC).

The maximum likelihood estimate of the shift parameter can probably be shown to be the minimum value observed in the data. As such something like the following can be used to obtain the maximum likelihood estimates:

p = 3;
a = Table[α[j], {j, 1, p - 1}];
b = Table[λ[j], {j, 1, p}];

(* Estimate of shift parameter *)
shift = Min[simData] - 0.001

(* Estimate remaining parameters *)
sol = NMaximize[{LogLikelihood[CoxianDistribution[a, b], simData - shift],
  0 <= a <= 1 && b >= 0}, Flatten[{a, b}], MaxIterations -> 1000]
(* {-2020.24, {α[1] -> 0.962951, α[2] -> 0.999625, λ[1] -> 0.843055, 
   λ[2] -> 0.843053, λ[3] -> 0.843294}} *)

(* Calculate AIC to allow for comparisons among different values of p *)
aic = -2 sol[[1]] + 4 p

(I subtracted 0.001 from the minimum of the data so that LogLikelihood function wouldn't complain about a zero.) I took just the first 1,000 of your 12,000 data values and it took about 1 minute to find the estimates. Doing all 12,000 is likely to take a lot more than 12 times that amount of time. (Do you really need 12,000 observations?)