Matching timestamped data

Question

I bet this question is a gimme for most of you guys, but I'm having a bit o' trouble figuring it out. Thanks ahead of time for your input and help.

Soooo, I have two datasets where column 1 is a timestamp and column 2 is the data point at that time step. My timestamps have been converted to AbsoluteTime to make things easier. Since my datasets start at different times of year, I would like to be able to sync them up via timestamps so I can perform calculations on them.

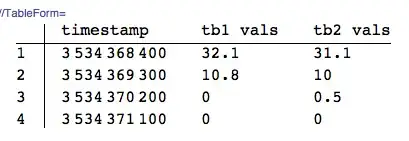
s1 = {{3534364800, 0}, {3534365700, 0}, {3534366600, 12.3}, {3534367500, 53.8}, {3534368400, 32.1}, {3534369300, 10.8}, {3534370200, 0}, {3534371100, 0}};
s2 = {{3534368400, 31.1}, {3534369300, 10}, {3534370200, .5}, {3534371100, 0}, {3534372000, 15.2}, {3534372900, 8.8}, {3534373800, 0}, {3534374700, 0}};

Small snippet of the code. Essentially I would like the code to match up the timestamps, so the the first set needs to match up with the second set.

Are you looking for exact matches of the timestamps or within some tolerance / interval ? — Anton Antonov, Mar 07 '16 at 15:46

score 2 · Accepted Answer · answered Mar 07 '16 at 16:53

Data tables from the question:

tb1 = {{3534364800, 0}, {3534365700, 0}, {3534366600, 12.3}, {3534367500, 
    53.8}, {3534368400, 32.1}, {3534369300, 10.8}, {3534370200, 
    0}, {3534371100, 0}};
tb2 = {{3534368400, 31.1}, {3534369300, 10}, {3534370200, .5}, {3534371100, 
    0}, {3534372000, 15.2}, {3534372900, 8.8}, {3534373800, 0}, {3534374700, 
    0}};

Indexes to demonstrate the matching:

index1 = AssociationThread @@ Transpose[tb1];
index2 = AssociationThread @@ Transpose[tb2];

Common tiimestamps:

commonTS = LongestCommonSequence[tb1[[All, 1]], tb2[[All, 1]]]

(*{3534368400, 3534369300, 3534370200, 3534371100}*)

Joined data tables:

TableForm[Transpose@{commonTS, index1 /@ commonTS, index2 /@ commonTS}, 
 TableHeadings -> {Automatic, {"timestamp", "tb1 vals", "tb2 vals"}}]

score 1 · Answer 2 · answered Mar 07 '16 at 16:49

Perhaps you should use the TimeSeries construct instead of messing with the raw data.

For instance, convert your lists to two TimeSeries objects:

ts1 = TimeSeries[{DateList[#1], #2} & @@@ {{3534364800, 0}, {3534365700, 0}, 
         {3534366600, 12.3}, {3534367500, 53.8}, {3534368400, 32.1}, {3534369300, 10.8}, 
         {3534370200, 0}, {3534371100, 0}}
      ]

ts2 = TimeSeries[{DateList[#1], #2} & @@@ {{3534368400, 31.1}, {3534369300, 10}, 
         {3534370200, .5}, {3534371100, 0}, {3534372000, 15.2}, 
         {3534372900, 8.8}, {3534373800, 0}, {3534374700, 0}}
      ]

ts1 ts2

As you can see, they are automatically aligned:

Mathematica graphics

You can then perform mathematical operations on the TimeSeries objects: the operations will only be performed in those regions where both TimeSeries coincide:

ts1 - ts2

difference

You can more clearly see the results of this operation by looking at the values directly:

ts1 - ts2 // Normal

normal form

And the difference can be plotted directly as well:

DateListPlot[ts1 - ts2]

difference plot

Matching timestamped data

2 Answers2