Interactive Application using Manipulate for Fibonacci Series

Question

I am working on creating interactive app using Manipulate function on fibonacci series using SeriesCoefficient. I want to plot the fibonacci numbers based on the slider of Manipulate function.

I have:

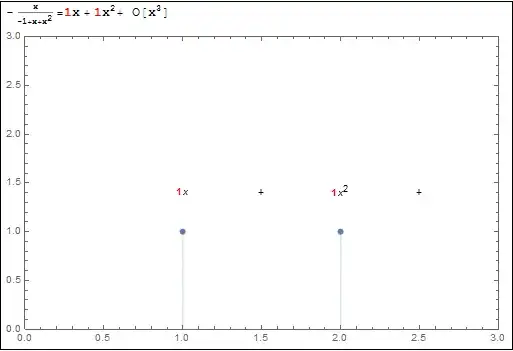
SeriesCoefficient[-(x/(-1 + x + x^2)), {x, 0, n}]

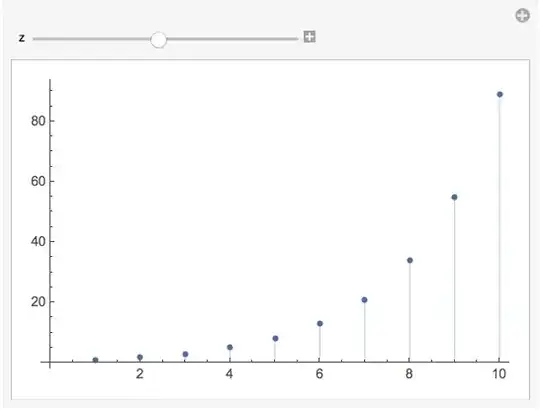
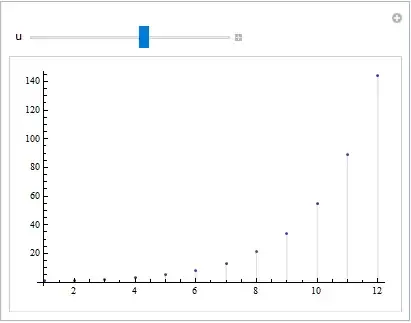
I want to use Manipulate function on the result of the above function and want to create discrete plot based on that. Is it possible to do that, please let me know.

Answer 1

Is this what you want?

Manipulate[
 ListPlot[
  Map[
  SeriesCoefficient[Series[1/(1 - x - x^2), {x, 0, 10}], #] &, 
   Range[z]], Filling -> Axis],
  {z, 1, 20, 1}]

---

u might like this representation:

fib[0] := 1
fib[1] := 1
fib[n_] := fib[n - 1] + fib[n - 2]

Manipulate[ListPlot[Map[fib, Range[z]]], {z, 1, 20, 1}]

---

here is a 'light version' of the code at the top.

Manipulate[
SeriesCoefficient[Series[1/(1 - x - x^2), {x, 0, 10}], z], {z, 1, 20,
1}]

Answer 2

Just for fun:

fun[num_] := 
 Module[{s}, s = Normal@Series[-(x/(-1 + x + x^2)), {x, 0, num}];
  s /. {x :> Row[{Style[1, Red, Bold], x}], 
    x^n_ :> Row[{Style[1, Red, Bold], x^n}], 
    a_ x^n_?NumericQ :> Row[{Style[a, Red, Bold], x^n}]}]
vis[n_] := Module[{ser = fun[n], tab},
  tab = Table[{Text[ser[[j]], {j, Fibonacci[j] + 0.2 n}], 
     Text["+", {j + 1/2, Fibonacci[j] + 0.2 n}]}, {j, 1, n}];
  ListPlot[Fibonacci@ Range[n], Filling -> Axis, Epilog -> tab, 
   PlotRange -> {{0, n + 1}, {0, Fibonacci[n] + n}}, Frame -> True, 
   ImageSize -> 500]]
v[n_] := Column[{Row[{-(x/(-1 + x + x^2)), "=", fun[n], "+ O[", 
     x^(n + 1), "]"}],
   vis[n]}, Frame -> True]

Visualizing:

Answer 3

Manipulate[ListPlot[Fibonacci[Range[u]], Filling -> Axis], {u, 1, 20, 1}]

or

Manipulate[DiscretePlot[Fibonacci[t], {t, 1, u, 1}, Filling -> Axis], {u, 1, 20, 1}]

or

Manipulate[DiscretePlot[SeriesCoefficient[Series[x/(1 - x - x^2), {x, 0, u}], t], 
 {t, 1, u, 1}, Filling -> Axis], {u, 1, 20, 1}]

to get