How to tell Solve[] to satisfy as many constraints as it can?

Question

Is there any way to tell Solve (or something similar) to return values for variables that solved as many constraints as it happened to satisfy?

Edit:

I had trouble finding a small example that wasn't trivial, but I finally did. Here's one:

Solve[{{-1 + Abs[q2 (-(7/4) + t1)], q1, -1 + Abs[q1 (-(7/4) + t2)], 3 + q2} == 0,
       {t1, t2} >= 7/4},
      {t1, t2, q1, q2}]

The kind of output that I want (I don't care if it's not unique; I can deal with that):

{{t1 -> 25/12, t2 -> Indeterminate, q1 -> 0, q2 -> -3}}

The output that I get, but don't want:

{}

Answer 1

If your equations and constraints are linear (or can be expressed as linear), and if a machine precision solution is enough you can use functions like LinearProgramming or NMinimize to get a solution:

M = 50;
NMinimize[{
  z1 + z2 + z3,
  {
   -1 + Abs[q2 (-(7/4) + t1)] == 0,
   q1 == 0,
   -1 + Abs[q1 (-(7/4) + t2)] >= 0 - M*z3,
   -1 + Abs[q1 (-(7/4) + t2)] <= 0 + M*z3,
   3 + q2 == 0,
   t1 >= 7/4 - z1*M,
   t2 >= 7/4 - z2*M,
   z1 \[Element] Integers, 0 <= z1 <= 1,
   z2 \[Element] Integers, 0 <= z2 <= 1,
   z3 \[Element] Integers, 0 <= z3 <= 1
   }
  },
 {t1, t2, q1, q2, z1, z2, z3}
 ]

{2., {t1 -> 2.08333, t2 -> 549.224, q1 -> 0, q2 -> -3., z1 -> 1, z2 -> 1, z3 -> 0}}

Basically, you introduce some binary ($0-1$) decision variables $z_i$ and one or more costant $M$ big enough so that you can rewrite the desired $i$ constraint in a way that when $z_i$ is $1$ constraint is always satisfied. You then minimze the sum of $z_i$.

More references to LinearProgramming in my answer here and

• Solving the magic backyard puzzle with MMA

and another example of "conditional constraints", here:

• Puzzle with Mathematica

With NMinimize you can also handle some non-linear constraint. Unfortunately Minimize is not available because:

Minimize::mixdom: Exact optimization with mixed real and integer variables is not yet implemented.

You can of course try to implement by yourself this strategy (a search on a suitable tree) to get an exact answer. If there are only few "conditional constraints" you can also try to Solve for all possible $(z_1z_2\ldots)$ until you find a solution. In this case, with at most $2^3=8$ cases is not too difficult.

---

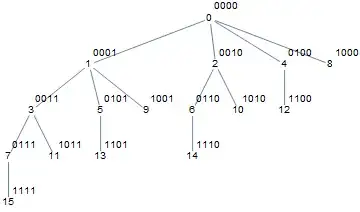
As an idea of how we can do a search on a tree, start building a suitable tree. This tree is such that the binary digits of the node are used to identify a subset of constraints. There is also an interesting ordering in DepthFirstScan visit order; see the picture.

vt[n_] := Module[{l, p},
  l = Range[0, 2^n - 1];
  p = FromDigits[#, 2] & /@ 
    Replace[IntegerDigits[l, 
      2], {a : 0 ..., 1, b___} :> {a, 0, b}, {1}];
  TreeGraph[l, p, VertexShapeFunction -> "Name", 
   VertexLabels -> Thread[l -> IntegerString[l, 2, n]]]
  ]
vt[4]

A simple (?), but far from optimal, search function is:

ssolve[eqns_, cons_, vars_, dom : _ : Reals] :=
 Module[{n, t, m, c, s, l, w, r},
  n = Length@cons;
  t = vt[n];
  s = Association@Thread[VertexList[t] -> False];
  m = -\[Infinity]; c = Indeterminate;
  r = {};
  DepthFirstScan[t, 0,
   "DiscoverVertex" -> Function[{u, v, d},
     Which[
      s[v], s[u] = True,
      d > m,
      With[{sol = 
         Quiet@Solve[
           Join[eqns, Pick[cons, IntegerDigits[u, 2, n], 1]], vars, 
           dom]},
       If[sol == {}, s[u] = True,
        c = u; r = sol; m = d
        ]]
      ]]];
  {Pick[cons, IntegerDigits[c, 2, n], 1], r}
  ]

A sample (all your equations and inequalities are considered optional):

eqns = Thread /@ {{-1 + Abs[q2 (-(7/4) + t1)], 
      q1, -1 + Abs[q1 (-(7/4) + t2)], 3 + q2} == 0, {t1, t2} >= 7/4} //
   Flatten
vars = {t1, t2, q1, q2};
ssolve[{}, eqns, vars, Reals]

The return value is a list with the set of constraints fulfilled and the return value of Solve.

{{-1 + Abs[q2 (-(7/4) + t1)] == 0, -1 + Abs[q1 (-(7/4) + t2)] == 0, 
  3 + q2 == 0, t1 >= 7/4, 
  t2 >= 7/4}, {{t1 -> ConditionalExpression[25/12, q1 > 0], 
   t2 -> ConditionalExpression[(4 + 7 q1)/(4 q1), q1 > 0], 
   q2 -> ConditionalExpression[-3, q1 > 0]}, {t1 -> 
    ConditionalExpression[25/12, q1 < 0], 
   t2 -> ConditionalExpression[(-4 + 7 q1)/(4 q1), q1 < 0], 
   q2 -> ConditionalExpression[-3, q1 < 0]}}}

I didn't fully tested the code but the basic idea should work, and should be more efficient than testing all the possible subsets of constraints. The use of built-in function DepthFirstScan is easy, but unfortunately at present doesn't allow to really skip the visit of a subtree.

Edit. In the way I used DepthFirstScan, nodes are not processed in DFS order. To fix this problem, I think a more involved code is required. At this point, I don't really see any reason to build a TreeGraph and use DepthFirstScan. I think it's better to use another strategy. I'll try to post an update when I have time.