How to approximate the solution of a system of quartic equations

Question

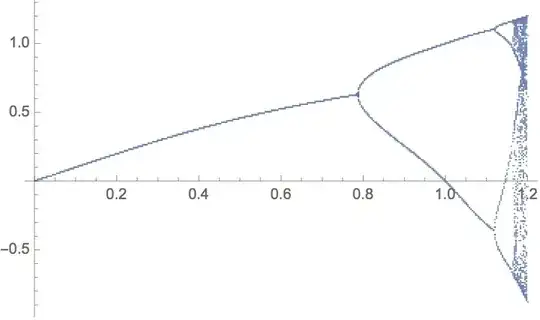
In an attempt to evaluate the point at which the cycle 2 becomes unstable for the given map:

\begin{equation} x_{n+1}=μ-x_n^4=f(x_n), \quad μ \in \mathbb{R} \end{equation}

I have so far managed to locate the two numerical values $\hat{x}_1, \hat{x}_2$ for which the period 2 trajectory appears:

Manipulate[Module[{list = NestList[μ - #^4 &, x0, 100]}, list2 = list;
Column[{ListLinePlot[list, PlotRange -> {-1, 1.5}, 
ImageSize -> {450, 375}], 
TableForm[Transpose@{Range[86, 101], list[[-16 ;;]]}, 
TableHeadings -> {None, {"point", "x"}}]}]], {{μ, 0.2, 
"parameter μ"}, 0, 4, 
Appearance -> "Labeled"}, {{x0, 0.4, 
"Initial \!\(\*SubscriptBox[\(x\), \(0\)]\)"}, 0, 1, 
Appearance -> "Labeled"}] 

But now I would like to locate the value of $μ$ for which this 2-cycle ceases to be stable and jumps onto the next one, a 4-cycle. The condition which has to hold is the following: \begin{equation} f'(\hat{x}_1)f'(\hat{x}_2)=-1 \Leftrightarrow 16\hat{x}_1^3 \hat{x_2}^3=-1 \end{equation} where $\hat{x}_i,i=1,2$ would be an expression of $μ$.

The problem is that Mathematica is not able to solve analytically the system: \begin{equation} \begin{cases} f(\hat{x}_1)=\hat{x}_2 \\ f(\hat{x}_2)=\hat{x}_1 \end{cases} \end{equation} in order to get the trajectory of the 2-cycle in a closed form, which will depend only on the parameter $μ$, which I can then plug it in the condition and find the value of that $μ$. What I get instead for

Reduce[{y == μ - z^4, z == μ - y^4}, {y, z}, Reals]

is the solution in Root form:

 ((μ == Root[27 + 256 #1^3 &, 1] && 
 y == Root[-μ + #1 + #1^4 &, 1]) || (Root[27 + 256 #1^3 &, 1] < 
 μ <= Root[-125 + 256 #1^3 &, 
 1] && (y == Root[-μ + #1 + #1^4 &, 1] || 
 y == Root[-μ + #1 + #1^4 &, 2])) || (μ > 
 Root[-125 + 256 #1^3 &, 1] && (y == Root[-μ + #1 + #1^4 &, 1] ||
 y == Root[
 1 - μ^3 - μ^2 #1 - μ #1^2 - #1^3 + 3 μ^2 #1^4 + 
 2 μ #1^5 + #1^6 - 3 μ #1^8 - #1^9 + #1^12 &, 1] || 
 y == Root[-μ + #1 + #1^4 &, 2] || 
 y == Root[
 1 - μ^3 - μ^2 #1 - μ #1^2 - #1^3 + 3 μ^2 #1^4 + 
 2 μ #1^5 + #1^6 - 3 μ #1^8 - #1^9 + #1^12 &, 2]))) && 
 z == -y^4 + μ

I understand that I am not able to solve this system analytically, but how can I then approximate this particular $μ$ value.

If I plug in the condition above the numerical values of $\hat{x}_1,\hat{x}_2$, I would have no $μ$ involved.

The point of this whole procedure is to calculate somewhow the universal $\delta$ Feigenbaum constant for this representative of the quartic equivalence class of discrete mappings.

Any help would be greatly appreciated. Thanks!

Answer 1

Let's start with a brute-force bifurcation diagram to see what's happening, modifying some code from @bbgodfrey's answer to this question:

f[x_, μ_] := μ - x^4;

res[μ_] := 
  DeleteDuplicatesBy[
   NestList[f[#, μ] &, Nest[f[#, μ] &, μ, 1000], 100], 
   Round[#, 10^-6] &];

ListPlot[Catenate[Table[{μ, #} & /@ res[μ], {μ, 0, 1.2, 0.001}]], 
 PlotStyle -> PointSize[Tiny], PlotRange -> All]

Looks like the μ you're looking for is near 1.1. To find a 2-cycle for a given μ numerically, we can try

μ = 1.05;
FindRoot[f[f[x, μ], μ] == x, {x, -0.5}]

(* {x -> -0.162297} *)

The bifurcation occurs when the two-cycle goes through a period-doubling bifurcation (eigenvalue=-1). We can numerically find the the bifurcation point by simultaneously solving for the two-cycle and when it loses stability:

Clear[μ];
FindRoot[{f[f[x, μ], μ] == x, D[f[f[x,μ], μ], x] == -1}, {x, -0.5}, {μ, 1.1}]

(* {x -> -0.359832, μ -> 1.11964} *)

Edit:

To generalize to higher order cycles (e.g. here's where the 4-cycle gives way to an 8-cycle):

FindRoot[{Nest[f[#, μ] &, x, 4] == x, D[Nest[f[#, μ] &, x, 4], x] == -1}, 
    {x, -0.64}, {μ, 1.16}]

(* {x -> -0.646515, μ -> 1.16166} *)

Of course it gets more delicate, so you'll probably want better initial guesses (which I got from looking at a zoomed-in version of the bifurcation diagram).

I don't know of any way to directly calculate the Feigenbaum constant here.

Edit 2:

I applied this approach to the first 7 period-doublings. The ratio of bifurcation points as in this wikipedia page looks like {7.90629, 7.25658, 7.3238, 7.28859, 7.28785}.