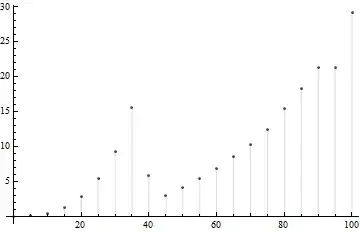
Here's a simple example for Solve:
test[f_] :=
ListPlot[Table[{n,
First@AbsoluteTiming@With[{c = Nest[f, c, n]}, Solve[c x^2 + x + 1 == 0, x]]},
{n, 0, 100, 5}], Filling -> Axis, PlotRange -> All]
test[Sqrt[c + #] &]
For any value of n, Solve is essentially dealing with the same equation, but the timing increases signifiantly as the coefficient c becomes more compilcated. Similar behavior can be observed in the tests for DSolve and RSolve. (I believe there're more.)
This truth astonishes me, because I thought Mathematica is clever enough to handle this sort of thing so I decide to write this post for complaining. To make this post a question, I want to ask:
Why Mathematica is cheated by the complicated coefficient?
Is there any general method to circumvent the issue? In my simple example, we just need to replace to only complicated coefficient with a simple one, but the coefficient to be replaced is not always obvious.
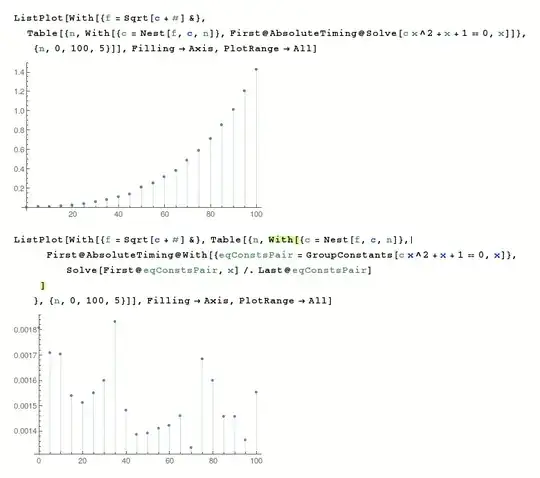
ConstantsGrouping`package](http://mathematica.stackexchange.com/a/103937/14303) would be useful here? – jkuczm Mar 11 '16 at 13:55