How to prevent extrapolation in Manipulate?

Question

How can I limit the time slider to the NDSolve solution range in a Manipulate box, so no extrapolation is used ? More specifically, here's a stripped down version of my Manipulate code which shows the problem :

X[t_] := {x[t], y[t], z[t]}
V[t_] := {x'[t], y'[t], z'[t]}
r[t_] := Norm[X[t]]
DipField[t_] := 3 ({0, 0, 1}.X[t]) X[t]/r[t]^5 - {0, 0, 1}/r[t]^3

Solution[v0_, theta_] := NDSolve[{
    x''[t] ==  Sqrt[1 - v0^2] {1, 0, 0}.Cross[V[t], DipField[t]],
    y''[t] ==  Sqrt[1 - v0^2] {0, 1, 0}.Cross[V[t], DipField[t]],
    z''[t] ==  Sqrt[1 - v0^2] {0, 0, 1}.Cross[V[t], DipField[t]],

    x[0] == 1, y[0] == 0, z[0] == 0, x'[0] == 0, y'[0] == v0 Sin[theta], z'[0] == v0 Cos[theta]
    }, {x, y, z}, {t, 0, 1000},
    Method -> Automatic, PrecisionGoal -> 7, MaxSteps -> 1000000,
    StoppingTest -> (r[t] < 0.1)]

Tmax[v0_, theta_] := (x /. Solution[v0, theta])[[1]][[1]][[1]][[2]]

Trajectory[t_, v0_, theta_] := ParametricPlot3D[Evaluate[X[s] /. Solution[v0, theta]], {s, 0.001, t}]

Manipulate[
    Show[
    Trajectory[t, v0, theta Pi/180],
    PlotRange -> {{-2, 2}, {-2, 2}, {-1, 1}},
    SphericalRegion -> True
    ],
{{t, 150, Style["Time", 10]}, 0, 200, 0.1},
{{v0, 0.25, "Velocity"}, 0, 1, 0.01},
{{theta, 63.3, "Polar angle"}, 30, 150, 0.1},
ControlPlacement -> Bottom
]

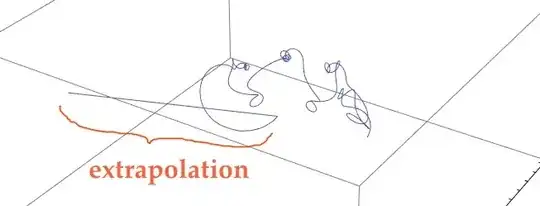
Here's a preview of the problem :

Currently, the Manipulate shows a part that comes from extrapolation, that shouldn't be there. The time slider should be limited to

Tmax[v0, theta]

but whathever what I'm trying in the time slider doesn't work.

EDIT : I'll try to be clearer. I solve some diff. equs using NDSolve, for time "t" going from 0 up to 1000. There's a contraint : NDSolve should stop if r[t] < 0.1. My code is doing this fine and finds a solution valid for 0 < t < Tmax[v0, theta] (I defined "Tmax" as a function of initial conditions).

Then I draw the solution using Manipulate, for all "t". Currently, the Manipulate code above is using all "t" up to 1000, which it shouldn't. For some initial conditions "v0" and "theta", Manipulate shows some extrapolation. The time slider must go instead from 0 up to Tmax(v0, theta). This is what I don't know how to do right.

EDIT 2 : The "duplicate" indicated above doesn't help much. I don't even see how it is related. The code shown there is so much different and much more complicated, it is not obvious at all to see how it may be related.

I don't see your problem, actually. Also your Tmax is fixed at 1000 as it simply the upper range of t as defined in the NDSolve. Your StoppingTest is an unknown option. This might be the cause of your problem. — Sjoerd C. de Vries, Mar 12 '16 at 19:48
@SjoerdC.deVries, NDSolve find a solution that must stop if r < 0.1. This isn't the cause of my problem, since the solution must stop at some time "Tmax <= 1000" (there's a singularity that I must avoid). Then time "t" is limited to Tmax, which depends on initial conditions. When I plot the curve, the time slider must be limited to this "Tmax", and this is what I don't know how to do. — Cham, Mar 12 '16 at 20:02
But what about this unknown option Stoppingtest? Why do you have it there? — Sjoerd C. de Vries, Mar 12 '16 at 20:04
The option Stoppingtest stops the numerical integration if r < 0.1 (is there a better way of doing this ? It's working perfectly with my version of MMA). I then find Tmax using the evaluation (x /. Solution[v0, theta])[[1]][[1]][[1]][[2]]. This is the time limit I must use in the Manipulate box. — Cham, Mar 12 '16 at 20:05
This option is unknown to Mathematica. At least, in my version 10.4 it is colored in red and not present in the documentation. I believe that it might have been there in version 3-5 or so, more than 10 years ago, but currently one would use WhenEvent. — Sjoerd C. de Vries, Mar 12 '16 at 20:15
That's a minor detail. The idea is that NDSolve finds a solution valid for t > 0 but t < Tmax (because of the constraint r > 0.1). Then you need to use Tmax as the time limit value for the time slider in the Manipulate box. This is what I don't know how to do. — Cham, Mar 12 '16 at 20:18
It doesn't seem like a detail to me. If the stoppingtest doesn't work because it's not an actual option then Tmax will always be 1000. — Sjoerd C. de Vries, Mar 12 '16 at 20:20
The stoppingtest do works for me. If it's not working for your version, then just replace it with the WhenEvent (which is unknown to my version). Then NDSolve will find a solution constrained by r > 0.1, and thus t < Tmax. — Cham, Mar 12 '16 at 20:22
If you don't use a WhenEvent to constraint the solution, you may find solutions that hit the central singularity. Time "t" cannot go up to 1000 for all solutions. — Cham, Mar 12 '16 at 20:24
@MichaelE2, the codes you're pointing to are much different and much more complicated than the MWE I gave above, and I don't see what part is pertinent to my problem. Please, could you be more specific ? — Cham, Mar 12 '16 at 21:02
Could you try adding the option "ExtrapolationHandler" -> {Indeterminate &, "WarningMessage" -> False} to NDSolve? (if you have a reasonably recent version of Mathematica) — Sjoerd C. de Vries, Mar 12 '16 at 21:23
@SjoerdC.deVries, in my version7, your command doesn't seem to be recognized. Also, this isn't related to my problem. Please, read the edit in my question. — Cham, Mar 12 '16 at 21:27
Does Manipulate[If[t > Tmax[v0, theta], t = Tmax[v0, theta]]; Show[Trajectory[t, v0, theta Pi/180], PlotRange -> {{-2, 2}, {-2, 2}, {-1, 1}}, SphericalRegion -> True], {{t, 150, Style["Time", 10]}, 0, Tmax[v0, theta], 0.1}, {{v0, 0.25, "Velocity"}, 0, 1, 0.01}, {{theta, 63.3, "Polar angle"}, 30, 150, 0.1}, ControlPlacement -> Bottom] work for you? — Sjoerd C. de Vries, Mar 12 '16 at 21:50
The code works partially : I'm getting a warning message : "The specified setting for the option FEFloatIterator cannot be used." And the time slider is all in red. — Cham, Mar 12 '16 at 22:11
@MichaelE2, well, I just made a search and got two results. I don't see how they are related to my problem. — Cham, Mar 12 '16 at 22:23
I'm still unable to define a proper max value for the time slider, without going in the extrapolation zone for some solutions. Maybe there's another way of defining the maximum allowed value for "t" ? — Cham, Mar 12 '16 at 22:33
Hmm, in @SjoerdC.deVries snippet, we forgot to convert degrees to radians : Tmax[v0, theta Pi/180]. Now the snippet code "works", except that moving the sliders is now very slow and laggy, even after aqdding SynchronousUpdating -> False. — Cham, Mar 12 '16 at 22:58

Cham · Answer 1 · 2016-03-13T01:04:23.567

This is a partial answer only, and need some fixes. The code below is working and prevent the interpolate part of some solutions. However, the interactivity is slow and laggy, even with the SynchronousUpdating -> False option. If the StoppingTest option doesn't work for you, just replace it with some WhenEvent translation, which isn't working with my version 7 :

X[t_] := {x[t], y[t], z[t]}
V[t_] := {x'[t], y'[t], z'[t]}
r[t_] := Norm[X[t]]
DipField[t_] := 3 ({0, 0, 1}.X[t]) X[t]/r[t]^5 - {0, 0, 1}/r[t]^3

Solution[v0_, theta_] := NDSolve[{
x''[t] == Sqrt[1 - v0^2] {1, 0, 0}.Cross[V[t], DipField[t]],
y''[t] == Sqrt[1 - v0^2] {0, 1, 0}.Cross[V[t], DipField[t]], 
z''[t] == Sqrt[1 - v0^2] {0, 0, 1}.Cross[V[t], DipField[t]],
x[0] == 1,
y[0] == 0,
z[0] == 0,
x'[0] == 0,
y'[0] == v0 Sin[theta],
z'[0] == v0 Cos[theta]
}, {x, y, z}, {t, 0, 1000}, Method -> Automatic, 
PrecisionGoal -> 7, MaxSteps -> 1000000, 
StoppingTest -> (r[t] < 0.1)]

(* This line below is the maximum time allowed for the solution : *)
Tmax[v0_, theta_] := (x /. Solution[v0, theta])[[1]][[1]][[1]][[2]]

Trajectory[t_, v0_, theta_] := ParametricPlot3D[Evaluate[X[s]/.Solution[v0, theta]], {s, 0.001, t}]

Manipulate[
    If[t > Tmax[v0, theta Pi/180], t = Tmax[v0, theta Pi/180]];
    Show[Trajectory[t, v0, theta Pi/180],
        PlotRange -> {{-2, 2}, {-2, 2}, {-1, 1}},
        SphericalRegion -> True],
{{t, 150, "t"}, 0, Tmax[v0, theta Pi/180], 0.1,
    ImageSize -> Large, Appearance -> {"Labeled", "Open"}},
{{v0, 0.25, "Velocity"}, 0, 1, 0.01,
    ImageSize -> Large, Appearance -> {"Labeled", "Open"}},
{{theta, 63.3, "Polar angle"}, 30, 150, 0.1,
    ImageSize -> Large, Appearance -> {"Labeled", "Open"}},
ControlPlacement -> Bottom, SynchronousUpdating -> False]

Now, how can we fix the low performances of this code ?

Compile, and then try to move the Velocity slider. The time slider will update itself in some occasions, but it's very slow and laggy ! Without the SynchronousUpdating -> False option, it's even worst.

EDIT : I may have found the solution and it is very simple. Just remove the Tmax from the time slider definition :

 {{t, 150, "t"}, 0, 1000, 0.1,
      ImageSize -> Large, Appearance -> {"Labeled", "Open"}},

The condition at the beginning of Manipulate appears to be enough to prevent the forbiden zone :

If[t > Tmax[v0, theta Pi/180], t = Tmax[v0, theta Pi/180]];

The time slider limit doesn't change, but at least the time selected adapt itself to prevent the extrapolation.

How to prevent extrapolation in Manipulate?

1 Answers1