Force WhenEvent to respect default stepsize

Question

I have to numerically integrate an equation system and monitor the accumulating datapoints. For example, I fit a line to a subsample of the points and terminate via "StopIntegration" if fitted line has ~0 slope. However, when I define a regular sampling time for WhenEvent (Mod[t, 1]), the collected log values have huge errors.

ode = {
   x'[t] == -.2 x[t]^2 + 2 y[t],
   y'[t] == x[t] + .1 x[t]^2 - 1.5 y[t],
   x[0] == y[0] == 1,
   WhenEvent[Mod[t, 1] == 0, 
    If[140 < t < 200, AppendTo[events, {t, Log@x@t}]]]
   };

events = steps = {};
if = NDSolveValue[ode, {x, y}, {t, 0, 200}, StepMonitor :> AppendTo[steps, {t, Log@x@t}]];

LogPlot[Through@if@t, {t, 0, 200}, Epilog -> {
   {Blue, AbsolutePointSize@6, Point@steps},
   {Red, AbsolutePointSize@3, Point@events}
   }, ImageSize -> 500]

I can see two ways to overcome this. 1) Set a method for NDSolve with uniform known stepsize and make the WhenEvent test at the same times. For certain reasons I want to avoid this. For one, it's nice to rely on the automatic adaptive stepsize algorithm. 2) Force WhenEvent to only evaluate when an internal step is taken by the integrator without modifying the step size manually. I failed to achieve this reliably. How to do this?

As you can see, it's perfectly unnecessary to increase accuracy/precision, as at steps the solution values are correct and I don't need to have extra values in between them. Note, that I cannot use StepMonitor solely, as I have to stop integration when a condition is met (based on the collected points).

Details

The problem is in the way Mathematica calculates solution values but not via the actual integrator method: when a value is calculated, WhenEvent interface does not know where the next point will be, so it has to extrapolate. It just does it in a horrible way. Somewhere in the process the actual derivative is lost, or even worse, a constant derivative is assumed, resulting in wild errors. See the following, even simpler example:

Block[{events = {}, steps = {}, if, x, t},
   if = NDSolveValue[{x'[t] == -1/10 x[t], x[0] == 1, 
      WhenEvent[Mod[t, #] == 0., AppendTo[events, {t, x[t]}]]}, 
     x, {t, 0, 100},
     StepMonitor :> {AppendTo[steps, t]}, 
     Method -> "ExplicitRungeKutta"(*,WorkingPrecision -> 50*)];
   Plot[if@t, {t, 0, 100}, 
    Epilog -> {Green, Point@events}, 
    PlotRange -> {All, {1, -1}}, GridLines -> {steps, {0}}, 
    PlotLabel -> Row@{"d = ", #}]
   ] & /@ {10, 1, 1/10, 1/100}

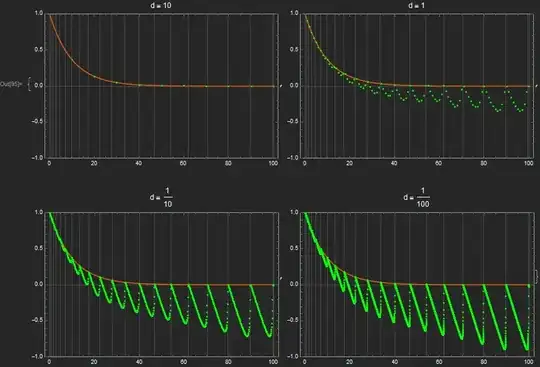
Vertical gridlines indicate internal steps, green points are the detected events. If you uncomment the option WorkingPrecision -> 50, the result is what one would expect - at the cost of at least double time required and I had to convert all reals to exact numbers.

Update

According to TechSupport, there is no way at the moment to evaluate a WhenEvent test only when the integrator takes a step. Maybe in a future version.

Answer 1

This is interesting even if it's not a perfect answer. It makes me suspect a bug somewhere.

I thought, for reasons that elude me -- it just occurred to me to try -- of enforcing a certain checking of x[t] by adding a "trivial" discrete variable and updating it from time to time. It is trivial in the sense that it never changes value and does not affect the OP's system. I guess in part I thought the variable would force NDSolve to track it, and perhaps x[t] would be calculated instead of extrapolated (for it seemed that extrapolation might be the explanation of the bad values for x[t] in the OP's code). So I changed the first DE to

x'[t] == -.2 x[t]^2 + 2 y[t] + a[t]

where a[t] == 0. I was able to get what I wanted by changing the event action

WhenEvent[Mod[t, 1] == 0, 
 If[140 < t < 200, AppendTo[events, {t, Log@x@t}], a[t] -> 0]]

But that was a typo. I meant to try the following which did not work:

WhenEvent[Mod[t, 1] == 0, 
 If[140 < t < 200, AppendTo[events, {t, Log@x@t}]; a[t] -> 0]]

I couldn't (and still cannot) explain why one worked and the other failed. I got the following, respectively:

Then I thought, what if the discrete variable a[t] was update periodically, but not very often, so that the OP's goal of letting the step size grow somewhat large might might be realized. This is, admittedly, similar to @user21's approach with MaxStepSize, but that approach still had "extrapolation" errors, albeit much smaller. This is unlike what a[t] -> 0 produced above (left image):

According to my speculative theory, an event of the form WhenEvent[Mod[t, dt] == 0, a[t] -> 0], might cause x[t] to be assigned the correct value. (I was beginning to think that extrapolation is not the reason for the wild values in the OP's code.) With dt = 10 or 20 everything seems to work fine. The value chosen for dt seemed to affect the step size (because NDSolve is worried that some discontinuous change to the ODE is going to occur at such an event). So I thought, how large can I make dt? I found that around 85, strange things happen.

ode2 = {x'[t] == -.2 x[t]^2 + 2 y[t] + a[t], 
   y'[t] == x[t] + .1 x[t]^2 - 1.5 y[t],
   a[0] == 0, x[0] == y[0] == 1, 
   WhenEvent[Mod[t, 1] == 0, 
    If[140 < t < 200, AppendTo[events, {t, Log@x@t}](*,a[t]->0*)]],
   WhenEvent[Mod[t, dt] == 0, a[t] -> 0]};

Table[
   events = steps = {};
   if = NDSolveValue[ode2, {x, y}, {t, 0, 200}, 
     StepMonitor :> AppendTo[steps, {t, Log@x@t}], 
     DiscreteVariables -> {a}];
   LogPlot[Through@if@t, {t, 0, 200}, 
    Epilog -> {{Blue, AbsolutePointSize@6, Point@steps}, {Red, 
       AbsolutePointSize@3, Point@events}}, ImageSize -> 250, 
    PlotLabel -> HoldForm[dt] == dt],
   {dt, 85, 88}
   ] // Partition[#, 2] & // GraphicsGrid

Three of the plots are have no error message; the upper right one has this error:

Coordinate {171., Complex[0.38451996298641833`, 3.141592653589793]} should be a pair of numbers, or a Scaled or Offset form.

The error just means that the value of some x[t] are negative when dt = 86, which in not inconsistent with the graph of the solution. For dt = 85 or 88, the values of event seem accurate, but in the case of dt = 88, there's a little glitch in the solution. As I said, it appears to be buggy (unless someone can explain why this is to be expected).

In any case, adding a[t] -> 0 in

WhenEvent[Mod[t, 1] == 0, 
 If[140 < t < 200, AppendTo[events, {t, Log@x@t}], a[t] -> 0]]

seems to be a workaround, even though I cannot explain why it works. None of these events, it seems to me, should affect the computed solutions to x[t] and y[t]. But they do.

Answer 2

One way to do this is not to restrict NDSolve to use a fixed size method but to restrict the MaxStepSize

if = NDSolveValue[ode, {x, y}, {t, 0, 200}, 
   StepMonitor :> AppendTo[steps, {t, Log@x@t}], MaxStepSize -> 2];

So if you use WhenEvent[Mod[t, dt] == 0.... I'd think you want MaxStepSize -> dt

From the documentation of WhenEvent: Mod[t,dt]==0 sample at regular intervals dt in the time variable t. But perhaps I miss the point?

Answer 3

Here is a potential workaround, that works on the OP's MWE. We'll restart integration at the beginning of logging of events. Since I'm not sure why the OP's code fails, I'm not sure why this fixes it. It potentially adds a step at t == 140, and it causes NDSolve to calculate a new starting step size. It's hard to know whether this would slow things down in all cases, but it has a negligible effect on the number of steps in the OP's MWE. I'll log the steps in steps2 and events2 to compare with the OP.

ode = {x'[t] == -.2 x[t]^2 + 2 y[t], 
   y'[t] == x[t] + .1 x[t]^2 - 1.5 y[t], x[0] == y[0] == 1, 
   WhenEvent[Mod[t, 1] == 0, If[140 < t < 200, AppendTo[events2, {t, Log@x@t}]]], 
   WhenEvent[t == 140, "RestartIntegration"]};

events2 = steps2 = {};
if = NDSolveValue[ode, {x, y}, {t, 0, 200}, 
   StepMonitor :> AppendTo[steps2, {t, Log@x@t}]];

LogPlot[Through@if@t, {t, 0, 200}, 
 Epilog -> {{Blue, AbsolutePointSize@6, Point@steps2}, {Red, 
    AbsolutePointSize@3, Point@events2}}]

The steps are about the same, with an adjustment at the restart of integration.

NumberLinePlot[{steps[[All, 1]], steps2[[All, 1]]}, 
 GridLines -> {{140}, None}]

There is a small error between the computed solution and the event values:

With[{xif = First@if},
 maxerr = Max@Abs[Differences /@ MapAt[Log @* xif, events, {All, 1}]]
 ]
(*  3.81291*10^-10  *)

We can see that this does not really fix the error observed in the OP:

Show[
 plot = LogPlot[First[if][t], {t, 139, 200}], 
 Graphics[{{Blue, AbsolutePointSize@6, Point@steps2}, {Red, 
    AbsolutePointSize@3, Point@events2}}],
 PlotRange -> {{139, 200}, Last@PlotRange@plot + maxerr {-1, 1}}]

Note that the initial slopes of the event arcs are close to the derivative of x[t] at t == 140, where integration (re)started. A similar pattern may be observed in the OP. This is not strictly true, nor does it seem that each arc starts with the same rate of change.

SplitBy[Differences@Exp@events2[[All, 2]], Positive][[1 ;; ;; 2, 1]]
First[if]'[140]
(*
  {6.90459*10^-10, 6.54047*10^-10, 6.05088*10^-10, 6.11475*10^-10}
  7.31003*10^-10
*)

If the arcs are connected to x'[140], then this workaround may only work accidentally, as it were, in the OP's MWE.