How to realize a Fourier Transform on a non-uniform sampling data

Question

I have a non-uniform sampling data (in time domain) from a Michelson interference experiment, as shown in Fig 1. But it was not evenly sampled (the step length was not uniform), because of the imperfection in the experiment. Further, if we enlarge the figure, we can see some bad-sampled points in Fig. 2 (the plot of a[[3800 ;; 4300]]).

The horizontal axis is time in femto-second (10^-15 second). In frequency domain, the central wavelength is [Lambda] = 800 nm, and the corresponding central frequency should be c/[Lambda] = 3*10^8/(800*10^-9) = 3.75*(10^14) Hz.

    SetDirectory[NotebookDirectory[]];
    name = "try.txt";
    a = Import[name, "Table"];
    ListLinePlot[a, PlotRange -> All, Joined -> False, Mesh -> Full,    Axes -> False, Frame -> True, AspectRatio -> .75,  LabelStyle -> Directive[Black, FontSize -> 18], FrameLabel -> {{"Amplitude", None}, {"Time (fs)", None}},  ImageSize -> {400, 300}]

My question is : how to carry out a Fourier Transform on this time - domain data, so as to obtain the spectral distribution. Any suggestion or help will be highly appreciated. Thank you all in advance.

Answer 1

You can do an "irregular" Fourier transform by accounting for explicit horizontal axis values.

IFT[(w_)?NumberQ, vals_, times_] := 
 Total[vals*Exp[(-I)*w*times]]/Length[times]

As coded above this is slow but there are sampling theorem based methods that bring it closer to the FFT in terms of speed.

I removed the HTML parts and put the file "try.txt" into my /tmp directory.

data = Import["/tmp/try.txt", "Data"];
Dimensions[data]
{times, vals} = Transpose[data];

(* Out[1015]= {7469, 2} *)

First an overall picture.

Plot[Abs[IFT[w, vals, times]], {w, 0, 202}, PlotRange -> All]

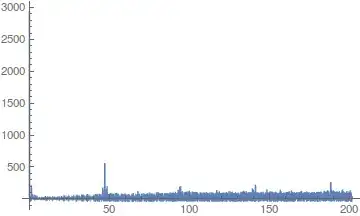
Besides what appears to be a DC component (hard to see since it is blue on black at the y axis), there seems to be a spikes located at a bit under 50, with smaller ones at multiples thereof. So we'll home in on that fundamental harmonic.

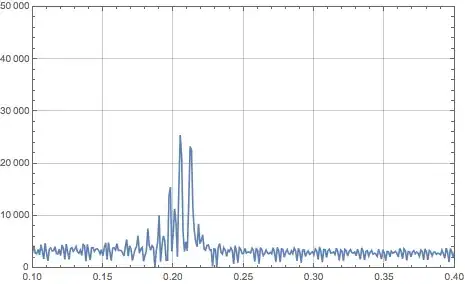
Plot[Abs[IFT[w, vals, times]], {w, 43, 52}, PlotRange -> All]

--- edit ---

Given the confusion (especially mine) over what is or might be the fundamental frequency, I did some more tests. The results might be of interest.

First I will remark that at frequency w=.2 (using the Exp[2*Pi*I*w...] normalization) I only get a small spike as compared to the larger one around 7.5. It's certainly noticeable in its neighborhood, but it's a very low-lying neighborhood.

Here is a good utility function. Given a putative period, it folds time values modulo that period. We will use it in ListPlot.

foldTimes[times_, period_] := period*FractionalPart[times/period]

I tried several values in the area of the peaks my IFT gave near .2 and the one below seemed to be among the more promising in terms of visibly showing something "periodic".

ListPlot[Transpose[{foldTimes[times, 1/(.209)], vals}]]

I will point out that using .204 instead of .209 gives a very different picture, but still one that looks "periodic". So I think we may have multiple and possibly incommensurate periods floating around. That said, I confess this visual analysis of signals is not a strong area for me.

Again with IFT redefined as below, we get a spike at 7.508, so we try the folded list plot using that reciprocal as putative period.

IFT[(w_)?NumberQ, vals_, times_] := 
 Total[vals*Exp[(2*Pi*I)*w*times]]/Length[times]

ListPlot[Transpose[{foldTimes[times, 1/7.508], vals}]]

So that period would seem to have separate the lefties from the righties. But why did we get lefties and righties in this signal? I have no idea (maybe it's an election year phenomenon). Anyway, thought it was sufficiently pronounced as to warrant mention and a picture.

--- end edit ---

--- edit 2 ---

Ack, I think all I did was approximate the "granularity" of the time steps. So it was all noise, literally and figuratively I guess. The smaller peak around .2 is real enough though.

--- end edit 2 ---

Answer 2

Let's prepare a data set that looks like the picture above.

t0 = -5;
t1 = 5;
delta = t1 - t0;
nPoints = 50000;
freq = 20.0;

f[x_] := (Sin[2 Pi freq x])/(x^2 + 1);
range = Sort@RandomReal[{t0, t1}, nPoints]; (* ordered list of non-uiform samples *)
data = Transpose@({#, f[#]} &@range);
ListLinePlot[data, Joined -> False, Frame -> True, Axes -> None, 
 GridLines -> Automatic, PlotRange -> Full]

Then make interpolation function and calculate its value on regular grid:

ifun = Interpolation[data];
sample = Table[{t0 + i/nPoints*delta, ifun[t0 + i/nPoints*delta]}, {i, 0, 
    nPoints - 1}];

After that we perform Fourier transform normally:

fdata = Abs@Fourier@(Transpose@sample)[[2]];
frange = N@(Range[0, nPoints - 1]/delta);

ListLinePlot[Transpose@{frange, fdata}, Frame -> True, Axes -> None, 
 GridLines -> Automatic, PlotRange -> {{0, 50}, Full}]

Regarding your second question, what do you want to do with those bad points? How do you know that they are bad?

Edit: To use OP's data

data = Import["try.txt", "Data"];
{t0, t1} = #[[1]] & /@ data[[{1, -1}]];
delta = t1 - t0
nPoints = Length@data
ListLinePlot[data, Joined -> False, Frame -> True, Axes -> None, 
 GridLines -> Automatic, PlotRange -> {Full, Full}]

ifun = Interpolation[data];
sample = Table[{t0 + i/delta, ifun[t0 + i/nPoints*delta]}, {i, 0, 
    nPoints - 1}];
fdata = Abs@Fourier@(Transpose@sample)[[2]];
frange = N@(Range[0, nPoints - 1]/delta);
ListLinePlot[Transpose@{frange, fdata}, Frame -> True, Axes -> None, 
 GridLines -> Automatic, PlotRange -> {{0.1, 0.4}, {0, 50000}}]