Let $T^2\cong S^1\times S^1$ be the one-holed torus surface (say, embedded in $\mathbb{R}^3$) and say I have a simple-ish map $f:T^2\to T^2$ which I'd like to visualize. How might I do that?
To make this concrete, let $f(z,w)=(zw,z^2)$ where $z,w\in S^1$. I'd like to see a decent representation of the image of this map on $T^2$.
Here's what I know:
From a previous answer here, I know I can visualize a torus in Mathematica (as well as plot a contour on it). For example, I can use something like
yourFunc = Function[{u, v}, Re[2 Exp[2 π I (u + 2 v)] + 3 Exp[2 π I (u - 2 v)]]];
ParametricPlot3D[{(2 + Cos[2 π v]) Sin[2 π u],
(2 + Cos[2 π v]) Cos[2 π u], Sin[2 π v]},
{u, 0, 1}, {v, 0, 1},
MeshFunctions -> Function[{x, y, z, u, v},
yourFunc[u, v]], Mesh -> {{0}},
MeshStyle -> Directive[Blue, Thick], PlotPoints -> 50]
to visualize (on a torus) the contour corresponding to the zero-set of a provided parametric function:
However, this sort of example hinges on a 3D parametric representation of a torus rather than a product of circles representation and my knowledge is currently insufficient to bridge the gap.
Edit: Per a comment by @Rahul below: I'm considering $S^1$ as a subset of $\mathbb{C}$. In particular, the map $f(z,w)$ can be converted to a map $[0,1]^2\mapsto[0,2]^2$ by converting:
$$z=e^{2\pi i\theta},w=e^{2\pi i \phi}\implies zw=e^{2\pi i(\theta+\phi)}\text{ and }z^2=e^{2\pi i(2\theta)}.$$
So, equivalently, we have a map $g:[0,1]^2\to[0,2]^2$ given by $g(\theta,\phi)=(\theta+\phi,2\theta)$. Using Mod, we can visualize a parametric plot for the map $g$:
ParametricPlot[{Mod[u + v, 1], Mod[2 u, 1]}, {u, 0, 1}, {v, 0, 1}]
yields
. Does this help? Note that I tried substituting
yourFunc = Function[{u, v}, {u+v, 2u}];
into the original snippet of code above but that doesn't work.


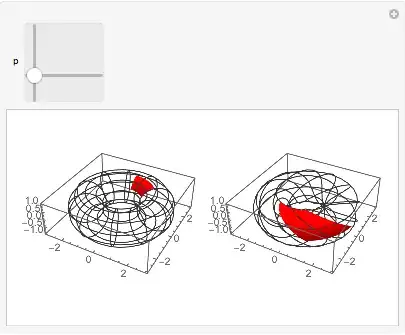

v==constand the second one has the path is the result of your mapping applied to the circle. You can also useManipulateto make an animation. Are you interested in this particular mapping? Or you want a general solution? – BlacKow Mar 16 '16 at 16:19