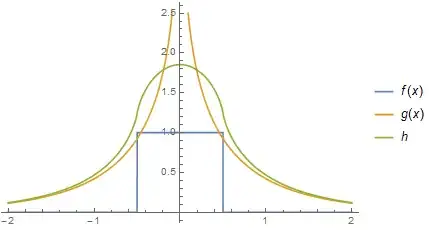
In 1D the convolution of the unit box function and the modified Bessel function of the second kind $K_0(x)$ works very well.
Clear[f, g, h];
f[x_] := UnitBox[x];
g[x_] := BesselK[0, Abs[x]];
h = Convolve[f[y], g[y], y, x]
Plot[{f[x], g[x], h}, {x, -2, 2}, PlotLegends -> "Expressions"]
However, when I try the same in 2D, the convolution doesn't work.
Clear[f, g, h];
f[x1_, x2_] := UnitBox[x1, x2];
g[x1_, x2_] := BesselK[0, Sqrt[x1^2 + x2^2]];
h = Convolve[f[y1, y2], g[y1, y2], {y1, y2}, {x1, x2}]
How can I solve this problem in 2D? I am only interested in the analytical solution.

h = Integrate[f[y1, y2] * g[x1-y1, x2-y2], {y1, -Infinity, Infinity}, {y2, -Infinity, Infinity}]doesn't work either. – Pavlo Fesenko Mar 17 '16 at 11:46PolyMap[n_, z_] := z Hypergeometric2F1[1/n, 2/n, (n + 1)/n, z^n]– yarchik Jul 17 '16 at 19:15