How to fill a region with lines

Question

How to fill a region with lines:

Plot[{t + 1, t}, {t, 0, 4}, PlotRange -> {0, 4},Filling -> {1 -> {2}}]

I want to change the filling style to vertical lines, as shown in the right figure below. How should I change the code?

In addition to the answe below, you may want to search this site for "hatched" or "hashed" filling. There have been a few examples, the best of which seem to rely on using a RegionPlot of the region and mesh lines. — MarcoB, Mar 21 '16 at 04:11
Welcome to Mathematica.SE! I suggest the following: 0) Browse the common pitfalls question 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Read the [faq]! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! — Dr. belisarius, Mar 21 '16 at 08:48
Strongly related: "Generating hatched filling using Region functionality." — Alexey Popkov, Mar 21 '16 at 08:57

Dr. belisarius · Answer 1 · 2016-03-21T07:11:36.713

funs = {t + 1, t};

Show[{Plot[funs, {t, 0, 4}, PlotRange -> {0, 4}], 
      RegionPlot[funs[[2]] < y < funs[[1]], {t, 0, 10}, {y, 0, 6}, 
                 Mesh -> 60, MeshFunctions -> {#1 &}, BoundaryStyle -> None, 
                 MeshStyle -> {Gray, Thickness[.001]}, PlotStyle -> Transparent]}]

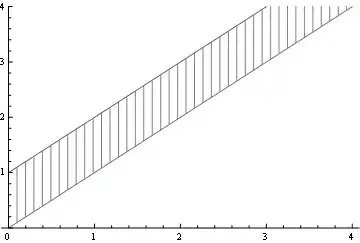
Mathematica graphics

Just for fun,to show the flexibility of this method:

Show[{Plot[funs, {t, 0, 4}, PlotRange -> {0, 4}], 
  RegionPlot[funs[[2]] < y < funs[[1]], {t, 0, 10}, {y, 0, 6}, 
   Mesh -> 60, MeshFunctions -> {Sin[#1] Sin[#2] &}, 
   BoundaryStyle -> None, MeshStyle -> {Gray, Thickness[.001]}, 
   MeshShading -> {Red, Green, None, Yellow}, 
   PlotStyle -> Transparent]}]

Mathematica graphics

score 10 · Answer 2 · answered Mar 21 '16 at 04:34

10

you could use GridLines also

Plot[{t + 1, t}, {t, 0, 4}, PlotRange -> {0, 4}, 
 GridLines -> {Range[0, 4, .2], None}, 
 Filling -> {1 -> {Top, White}, 2 -> {Bottom, White}}]

answered Mar 21 '16 at 04:34

Basheer Algohi

19,917
1
31
78

score 6 · Answer 3 · answered Mar 21 '16 at 04:10

I guess the simplest way is:

Show[
 ListPlot[{
   Table[i*2 + 1, {i, -1, 3, 0.1}],
   Table[i*2 + 3, {i, -1, 3, 0.1}]}, Joined -> True],
 ListPlot[{
   Table[i*2 + 1, {i, -1, 3, 0.1}],
   Table[i*2 + 3, {i, -1, 3, 0.1}]
   }, Joined -> False, Filling -> {1 -> {2}}, 
  PlotStyle -> PointSize[0.001]]
 ]

The point-based representation allows to have a discrete line-based filling.

garej · Answer 4 · 2016-03-21T07:06:43.783

4

A modification of Rom38's.

Show[
 Plot[{t + 1, t}, {t, 0, 4}, PlotRange -> {0, 4}],
 ListLinePlot[Table[{{i, i + 1}, {i, i}}, {i, 0, 4, 0.2}], PlotStyle -> {{Gray, Thin}}]
 ]

Another option with Epilog:

Plot[{t + 1, t}, {t, 0, 4}, PlotRange -> {0, 4}, 
 Epilog -> Table[Line @ {{i, i}, {i, i + 1}}, {i, 0, 4, 0.2}]]

edited Mar 21 '16 at 07:06

answered Mar 21 '16 at 06:26

garej

4,865
2
19
42

score 3 · Answer 5 · answered Mar 21 '16 at 08:06

3

Using Epilog

Plot[{t + 1, t}, {t, 0, 4}, 
 PlotRange -> {0, 4}, 
 Epilog -> Line /@ (Thread@{#, {# + 1, #}} & /@ Range[0, 4, 0.2])]

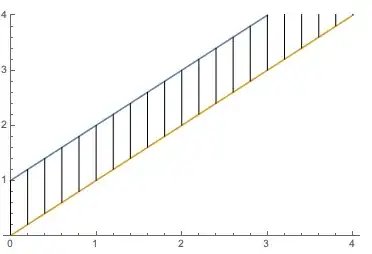
enter image description here

answered Mar 21 '16 at 08:06

xyz

605
4
38
117

score 2 · Answer 6 · answered Mar 21 '16 at 08:27

2

Here's yet another way to get what you are going for, by using ContourPlot

ContourPlot[#, {x, 0, 4}, {y, 0, 4}, ContourShading -> False, 
    Contours -> 20] & /@ {{x == y,
    x + 1 == y},
   Piecewise[{{x, x < y < x + 1}}, Indeterminate]} // Show

answered Mar 21 '16 at 08:27

Jason B.

68,381
3
139
286

How to fill a region with lines

6 Answers6