Want Manipulate to be low resolution enough to render fast but no so low resolution that it is useless

Question

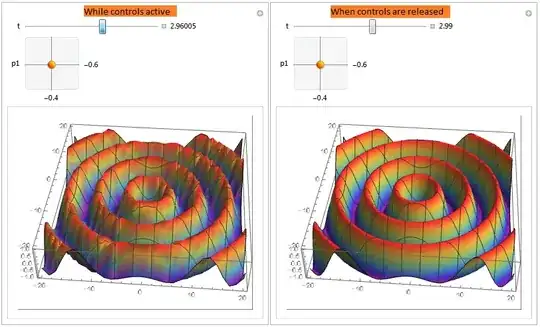
When using Manipulate to graph a simple surface (sum of 2 sine waves) with Plot3D, setting PerformanceGoal->"Quality" makes it take about 1/3 second to render, while "Speed" sets it at such a low resolution that you can't even see the general shape of the plot.

Is there a way to set the render quality to something in-between or to adjust how much rendering it does when set to "Speed"?

k = 1;
range = 20;
Manipulate[{Show[
   Plot3D[
    Sin[k*(Sqrt[(x - p1[[1]])^2 + (y - p1[[2]])^2] - t)],
    {x, -range, range}, {y, -range, range}, 
    BoxRatios -> Automatic, 
    ColorFunction -> "Rainbow"
   ]
  ]}, 
 {t, 0, 5}, 
 {p1, {-range, -range}, {range, range}}
]

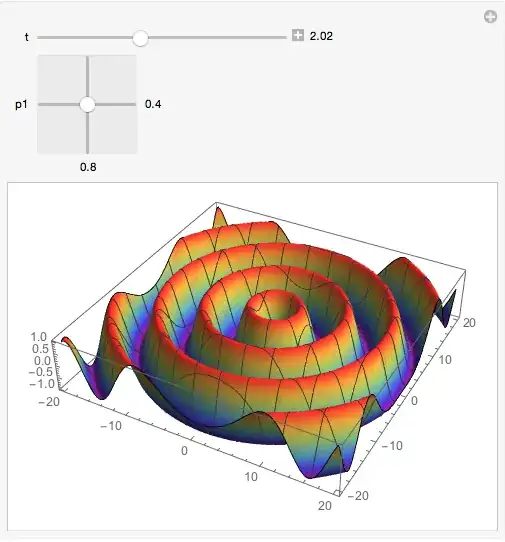
If you refrain from setting any PerformanceGoal, Manipulate should automatically adjust this parameter to have two different values, a speedy, low quality setting for when you are changing a parameter or rotating a plot, and a slower, higher quality setting used to "clean up" the plot when you let go of the controls. This works well e.g. in this: Manipulate[ Plot3D[Sin[3 x + 4 y] + Sin[4 x^2 - y^2], {x, y} \[Element] Rectangle[{0, 0}, {t, t}]], {{t, 1}, 0.1, 3} ], but right now you have us guessing at your problem. You should share your code so we can provide more specific help. — MarcoB, Mar 22 '16 at 03:32
I already tried that. The problem is that the speedy low quality is so low that the whole surface is just a vague blur until I release the mouse. — dsoodak, Mar 24 '16 at 04:46
code: k = 1; range = 20; Manipulate[{Show[ Plot3D[Sin[ k*(Sqrt[(x - p1[[1]])^2 + (y - p1[[2]])^2] - t)], {x, -range, range}, {y, -range, range}, BoxRatios -> Automatic, ColorFunction -> "Rainbow"]]}, {t, 0, 5}, {p1, {-range, -range}, {range, range}}] — dsoodak, Mar 24 '16 at 04:46
I was hoping that there would be a way to adjust the quality of the speedy setting to make it slightly higher quality — dsoodak, Mar 24 '16 at 04:54
Yes, I understand what you mean. Unfortunately I don't know how to accomplish what you want off the top of my head, but I'll look into this tomorrow. Thanks for providing a code sample. — MarcoB, Mar 24 '16 at 05:00
If your question gets reopened, I will post an answer, but basically you can get something like the performance compromise you want by increasing PlotPoints above the default. It will be system dependent, but I get reasonable results on my system by setting PlotPoints -> 50. — m_goldberg, Mar 24 '16 at 05:41
What @m_goldberg said.Set PlotPoints->50 and add the option Mesh->None. The result is quite speedy. One of you two should post a (self)answer now. PS Neither Show nor the curly braces around it are necessary. Just leave Plot3D as the first argument to Manipulate. — LLlAMnYP, Mar 24 '16 at 07:59

score 5 · Accepted Answer · answered Mar 24 '16 at 14:58

You can use ControlActive to fine-tune the behaviour of PlotPoints and PerformanceGoal while the variables are being manipulated.

With[{k = 1, range = 20}, 
 Manipulate[
  Plot3D[Sin[
    k*(Sqrt[(x - p1[[1]])^2 + (y - p1[[2]])^2] - t)], {x, -range, 
    range}, {y, -range, range}, Mesh -> 10, 
   PlotPoints -> ControlActive[30, 60], 
   BoxRatios -> {1, 1, .2}, 
   ColorFunction -> "Rainbow", 
   PerformanceGoal -> ControlActive["Speed", "Quality"]], 
  {t, 0, 5, Appearance -> "Labeled"}, {p1, 
  {-range, -range}, {range, range}, Appearance -> "Labeled"}
 ]]

Now while the controls are active (being manipulated) Plot3D will plot with PlotPoints->30 and PerformanceGoal->"Speed". However, once the controls are released Plot3D will do a finishing plot with PlotPoints->60 and PerformanceGoal->"Quality".

Hope this helps.

score 4 · Answer 2 · answered Mar 24 '16 at 14:13

You can get something like the performance compromise you ask for by increasing PlotPoints above the default. Graphics performance is system dependent, but I get reasonable results on my system by setting PlotPoints -> 50. You may need a different setting. Lowering the number of mesh points also helps. I used Mesh -> 10,.

Here is the modified version of your code that I found both responsive and pleasing to the eye.

With[{k = 1, range = 20},
  Manipulate[
    Plot3D[Sin[k*(Sqrt[(x - p1[[1]])^2 + (y - p1[[2]])^2] - t)], 
      {x, -range, range}, {y, -range, range},
      PlotPoints -> 50,
      Mesh -> 10,
      BoxRatios -> {1, 1, .2},
      ColorFunction -> "Rainbow"],
    {t, 0, 5, Appearance -> "Labeled"},
    {p1, {-range, -range}, {range, range}, Appearance -> "Labeled"}]]

Want Manipulate to be low resolution enough to render fast but no so low resolution that it is useless

2 Answers2