Your problem has little to do with Hold or any of its cousins. It has to do with the evaluator recursively evaluating symbols until it gets no changes. This can be demonstrated by using Trace.
x = a + b;
y = Hold[x*x] + x*c + d;
Trace[DeleteDuplicates @ Cases[y, _Symbol, -1]]

Note that Cases returned {a, b, c, d, x, x}, but then x got evaluated in the argument sequence passed to DeleteDuplicates, producing the result you don't want.
To get what you want you could do the following, using Block to locally make x a free variable.
x = a + b;
y = Hold[x*x] + Hold[x]*c + d;
Block[{x},
Trace[DeleteDuplicates@ Cases[y, _Symbol, -1]]]

But consider that if you assign y within the block, you don't need to worry about Hold.
x = a + b;
Block[{x},
y = x*x + x*c + d;
Trace[DeleteDuplicates @ Cases[y, _Symbol, -1]]]
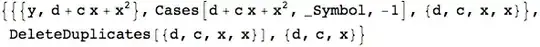
Update 1
As to why
y = Hold[x*x] + Hold[x]*c + d;
Cases[y, _Symbol, {-1}]
produces
{d, c, a + b, a + b, a + b}
rather than
{d, c, x, x, x}
This has a simple explanation. Cases actually returns {d, c, x, x, x}, but recall this is the short form for List[d, c, x, x, x]. Now List is function (although you may be thinking of it as a data type), so the evaluator evaluates this function call as well any other. The 2nd step in the evaluation cycle is to evaluate the function's argument, so of course x gets evaluated.
Update 2
After thinking this over for a while, it occurred to me that you might be interested in another approach to restricting evaluation. This will give a display form that meets your requirements.
y = ReleaseHold[Hold[x*x + x*c + d] /. HoldPattern[s : x | c | d] -> HoldForm[s]]
d + c x + x^2
y can still be evaluated with
y // ReleaseHold
(a + b)^2 + (a + b) c + d
but now
result = DeleteDuplicates @ Cases[y, HoldForm[_], {-2}]
gives
{d, c, x}
However, remember this is for display only. The internal form is
result // FullForm
List[HoldForm[d], HoldForm[c], HoldForm[x]]
Like y, result can be evaluated with ReleaseHold.



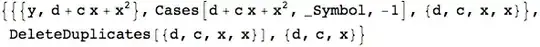


Variables. TryVariables@yinstead. – Edmund Mar 25 '16 at 12:46Variablesis promising, but it cannot totally solve this problem, it only works forpolynomial. Therefore, for general expression it won't work. E.g.Defer[x*x] + HoldForm[Sin[x]*c] + d. – Kattern Mar 25 '16 at 13:12