I have the following surface to plot $$(1-\frac{z^2}{4})^{16}=x^2+y^2$$
I decied to express $x$ as $x=x(y,z)$. And met the difficulty when combining 2 plots. Here is what I've done.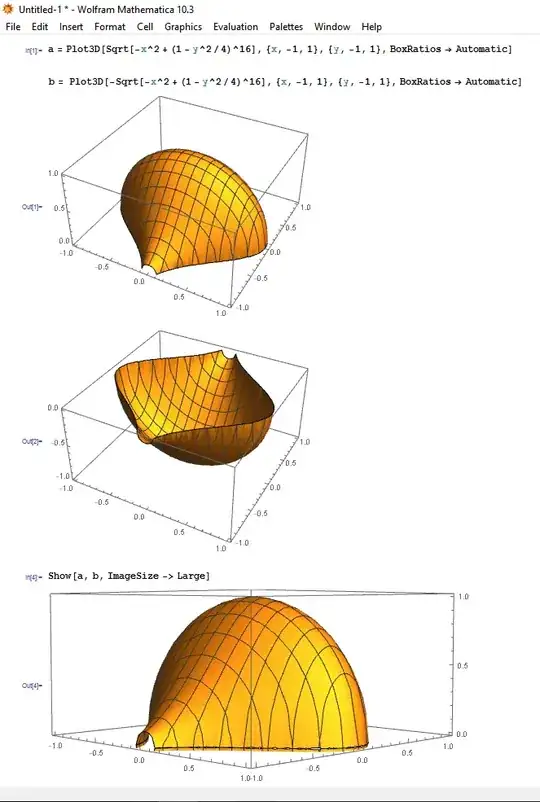
As u see I get only half a picture. Could somebody tell me what I am doing wrong and how to combine this 2 plots?
PlotRange-> {-1,1}as an option toShow. Does that fix it? – march Mar 25 '16 at 19:48Plot3D[{-1, 1} yourSqrtFunction, {x, -1, 1}, {y, -1, 1}]. – MarcoB Mar 25 '16 at 19:51PlotPoints -> 100toPlot3D. Play with the number ofPlotPointsuntil you get a smooth edge. – MarcoB Mar 25 '16 at 19:55ContourPlot3D[(1 - z^2/4)^16 - x^2 - y^2 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}]– Artes Mar 25 '16 at 19:57