A interesting question.Tom's family just have a flashlight which will extinguish after 30 seconds.They wanna go through a bridge to arrive opposite side with the flashlight.But as the picture,they need difference time to cross it alone.And a solw man with a faster man,the time depend on that slow man.The bridge only can bear two people at a time.They should how to cross it,then the time will be shortest?How to use method of graphs-and-networks to solve it?
A variant of the graph solution. I represent the flashlight as a sixth "person" with a crossing time of zero.
v = With[{s = Subsets[{0, 1, 3, 6, 8, 12}]}, Transpose[{Reverse@s, s}]];
f[{L1_, R1_}, {L2_, R2_}] := cross[R2 ⋂ L1, L2 ⋂ R1]
cross[LtoR : {0, Repeated[_, 2]}, {}] := Max[LtoR]
cross[{}, RtoL : {0, Repeated[_, 2]}] := Max[RtoL]
cross[__] := Infinity
g = WeightedAdjacencyGraph[v, Outer[f, v, v, 1]];
GraphDistance[g, First@v, Last@v]
(* 29. *)
Grid[FindShortestPath[g, First@v, Last@v], Alignment -> {{Right, Left}}]
Brief explanation
v is the list of vertices for the graph, it contains every possible way of splitting the six people (actually five people plus one flashlight) between the two sides of the bridge.f takes two such vertices and works out who must cross from left to right, and who from right to left, to change from the first configuration to the second. For example R2 ⋂ L1 is the set of people who are on the right side in configuration 2 and on the left side in configuration 1 - these people must cross from left to right.cross returns the crossing time for a step, which will be the edge weight in the graph. The allowed steps consist of one or two people plus the flashlight crossing in one direction, and nobody crossing in the other direction. Any other step is forbidden and gets an infinite time.f to each pair of vertices.{{0, 1, 3, 6, 8, 12}, {}} to the last {{}, {0, 1, 3, 6, 8, 12}}
Intersection.
– Aster
Nov 19 '17 at 05:04
Without graphs ... I don't see an easy way with them:
a = {1, 3, 6, 8, 12};
b = {};
go[{a_, b_, t_, c_}] := ({Complement[a, #], Join[b, #], t + Max@#, Append[c, #]} &/@
Subsets[a, {2}])
ret[{a_, b_, t_, c_}] := {Join[a, #], Complement[b, #], t + Max@#, Append[c, #]} &/@
Subsets[b, {1}]
gf[x_] := Flatten[go /@ x, 1];
rf[x_] := Flatten[ret /@ x, 1];
res = gf@rf@gf@rf@gf@rf[go /@ {{a, b, 0, {}}} // First];
Select[res, #1[[3]] <= 30 &][[All,3;;]]
(*
{{29, {{1, 3}, {1}, {6, 1}, {3}, {8, 12}, {1}, {3, 1}}},
{29, {{1, 3}, {1}, {6, 1}, {1}, {8, 12}, {3}, {1, 3}}},
{29, {{1, 3}, {1}, {8, 12}, {3}, {1, 6}, {1}, {3, 1}}},
{29, {{1, 3}, {1}, {8, 12}, {3}, {1, 3}, {1}, {6, 1}}},
{29, {{1, 3}, {3}, {8, 12}, {1}, {3, 1}, {1}, {6, 1}}},
{29, {{1, 3}, {3}, {8, 12}, {1}, {6, 1}, {1}, {3, 1}}},
{29, {{1, 6}, {1}, {3, 1}, {3}, {8, 12}, {1}, {3, 1}}},
{29, {{1, 6}, {1}, {3, 1}, {1}, {8, 12}, {3}, {1, 3}}}}
*)
Here you have it solved by using graph functions. I don't think you gain anything by doing it this way
a = {1, 3, 6, 8, 12}; int = Intersection; len = Length;
validTransitionFwd[{a_, _}, {x_, _}] := len@a - len@x == 2 && int[a, x] == x
validTransitionBkwd[{a_, _}, {x_, _}] := len@x - len@a == 1 && int[a, x] == a
transCost[{s1_, s2_}] := Max[Complement @@@ Transpose@{s1, s2}]
sa = Subsets[Flatten[{#, Reverse@#}&/@ ({Complement[a, #], #} & /@ Subsets@a), 1], {2}];
transitionsFwd = Thread[{{f, b}, #}] & /@ Select[sa, validTransitionFwd @@ # &];
transitionsBwd = Thread[{{b, f}, #}] & /@ Select[sa, validTransitionBkwd @@ # &];
g = Graph[DirectedEdge @@@ #, EdgeWeight -> transCost /@ #[[All, All, 2]]] &@
Union[transitionsBwd, transitionsFwd]
FindShortestPath[g, {f, {{1, 3, 6, 8, 12}, {}}}, {b, {{}, {1, 3, 6, 8, 12}}}][[All, 2]]
(*
{{{1, 3, 6, 8, 12}, {}},
{{6, 8, 12}, {1, 3}},
{{1, 6, 8, 12}, {3}},
{{1, 6}, {3, 8, 12}},
{{1, 3, 6}, {8, 12}},
{{6}, {1, 3, 8, 12}},
{{1, 6}, {3, 8, 12}},
{{}, {1, 3, 6, 8, 12}}}
*)
One more method without graphs is by using IntegerPartition.
For this particular problem there are 7 trips from start to end and let $t_1$ to $t_7$ represent those time. All $t_i \in \{1,3,6,8,12\}$.
Let $t_f$ be the total time. Then $t_f$ must partitions into 7 integers all of which belong to $\{1,3,6,8,12\}$.
If $t_f$ happens to be 30 then the result of
IntegerPartitions[30, {7}, {1, 3, 6, 8, 12}]
including all its Permutations will contain the time of the successful journey.
So the idea is to go over all permutations of these time and select only the ones which can fit the initial condition.
split2Bytime[list_, time_] :=
Module[{p1, p2, p3, p4, flag = 1, trip, pos, onwardPart, returnPart},
onwardPart = list[[3]];
returnPart = Last@list;
Which[Not@MemberQ[onwardPart, First@time], flag = 0, True,
Which[First@time == First@onwardPart, flag = 0, True,
pos = Flatten@Position[onwardPart, First@time];
p2 = onwardPart[[First@pos - 1 ;; First@pos]];
p3 = Reverse@TakeDrop[onwardPart, {First@pos - 1, First@pos}];
p4 = PadRight[Last@p3, Length[Last@p3] + Length@returnPart, returnPart];
trip[1] = Join[{First@p3}, {p4}];
Which[Not@DuplicateFreeQ[time],
p3 = Reverse@TakeDrop[onwardPart, {First@pos - 1}];
p4 = PadRight[Last@p3, Length[Last@p3] + Length@returnPart,returnPart];
trip[2] = Join[{First@p3}, {p4}];, True,
Which[Not@MemberQ[Last@trip[1], Last@time], flag = 0, True,
p3 = Insert[First@trip[1], Last@time, 1];
p4 = DeleteCases[Last@trip[1], Last@time];
trip[2] = Join[{p3, p4}];]]
];
];
If[flag == 1, Flatten[Array[trip, 2], 1], "failed"]
];
The function split2Bytime takes the initial list and two time values and throws the allowed configuration based on that time.
For e.g.
split2Bytime[{{}, {}, {1, 3, 6, 8, 12}, {}}, {2, 3}]
(*failed*)
will return failed because the time argument i.e. {2,3} represents the time taken for the first and second trip. But the first trip cannot take 2 units with
{{}, {}, {1, 3, 6, 8, 12}, {}} as the initial conflagration.
split2Bytime[{{}, {}, {1, 3, 6, 8, 12}, {}}, {3, 3}]
(*{{6, 8, 12}, {1, 3}, {3, 6, 8, 12}, {1}}*)
The above e.g. works because {3,3} is possible. The result is displayed as four sub-list where the first two part i.e. {6, 8, 12}, {1, 3} means {1,3} goes to the other side taking 3 seconds and the last two parts {3, 6, 8, 12}, {1} means that {3} comes back taking 3 seconds again.
splitAll[timings_] :=
Module[{flag = 1, last, trip, nlist = {{}, {}, {1, 3, 6, 8, 12}, {}}},
trip[1] = split2Bytime[nlist, timings[[1 ;; 2]]] // Quiet;
trip[2] = split2Bytime[trip[1], timings[[3 ;; 4]]] // Quiet;
trip[3] = split2Bytime[trip[2], timings[[5 ;; 6]]] // Quiet;
last = trip[3][[3]];
If[Not[Max@last == Last@timings] ||
Not[MemberQ[last, Last@timings]], flag = 0];
If[flag == 1, Array[trip, 3], "failed"]]
splitAll applies split2Bytime to all the timings 2 at a time and clubs them together at the end.
Now we can check for any total time $t_f$ whose integer partitions plus all its permutations satisfies splitAll.
check[n_] :=
Module[{sol, perms},
sol = IntegerPartitions[n, {7}, {1, 3, 6, 8, 12}];
perms =
Partition[
Flatten[Table[Permutations[sol[[i]]], {i, 1, Length[sol]}]], 7];
DeleteCases[
Table[If[
Not[ContainsAny[{splitAll[perms[[i]]]}, {"failed"}] ||
ContainsAny[splitAll[perms[[i]]], {"failed"}]], Sow[i]] //
Quiet, {i, 1, Length[perms]}], Null]]
check checks for all those Permutations which results in a failure. We can use it to see which ones are working. Lets check from 20 to 30
DeleteCases[Table[If[Not[check[n] == {}], Sow[n]], {n, 20, 30}], Null]
(*29*)
We get the correct total time $t_f=29$.
Now that we now $t_f=29$ we can display the full result of splitAll.
showResult[n_] :=
Module[{sol, result, perms, res, start = {{1, 3, 6, 8, 12}, {}}},
sol = IntegerPartitions[n, {7}, {1, 3, 6, 8, 12}];
perms =
Partition[
Flatten[Table[Permutations[sol[[i]]], {i, 1, Length[sol]}]], 7];
res = DeleteCases[
Table[If[
Not[ContainsAny[{splitAll[perms[[i]]]}, {"failed"}] ||
ContainsAny[splitAll[perms[[i]]], {"failed"}]], Sow[i]] //
Quiet, {i, 1, Length[perms]}], Null];
result[i_] :=
Partition[
Flatten[Append[Prepend[splitAll[perms[[res[[i]]]]], start],
Reverse@start], 1], 2];
Row[Table[Grid[result[i], Frame -> All], {i, 1, Length[res]}], " "]
]
As the help with many people in this post,I solve this proble with Graph Theory method.Build all possible in a graph based on the costed time on people:
time = {1, 3, 6, 8, 12};
people = StringReplace[ToString[time], " " -> ""];
seq[n_ /; n > 1] := Reverse[Riffle[Range[0, n - 2], Range[2, n]]]
Clear[exsited];
exsited[_] = False;
postfix =
Rest[If[exsited[#], StringJoin[ToString[#], ToString[Unique[]]],
exsited[#] = True; ""] & /@ seq[Length[time]]] //. {a___,
p : Except["", _String], "", b___} :> {a, p, p, b};
graphs = Function[{before, behind},
Graph[First[
WeaklyConnectedGraphComponents[
RelationGraph[
Equal[Length[#1], before] && Equal[Length[#2], behind] &&
SubsetQ @@ SortBy[{##}, -Length[#] &] &, Subsets[time]]]],
VertexLabels -> "Name", ImageSize -> 400]] @@@
Subsequences[seq[Length[time]], {2}];
Graph[graph =
GraphUnion @@
MapThread[
VertexReplace, {graphs,
Apply[If[
ToString[Length[#1]] === Quiet[First[StringSplit[#2, "$"]]],
Rule[#1,
StringReplace[StringJoin[{ToString[#1], #2}], " " -> ""]],
Rule[#1, StringReplace[ToString[#1], " " -> ""]]] &,
Tuples /@
Transpose[{VertexList /@ graphs, List /@ postfix}], {2}]}],
VertexLabels ->
Table[i -> First[StringSplit[i, RegularExpression["\\d+?\\$"]]], {i,
VertexList[graph]}], GraphLayout -> "LayeredDigraphEmbedding"]
FindShortestPath.weighGraph =
Graph[EdgeList[graph],
EdgeWeight ->
Table[i ->
Quiet[Max[
Complement @@
SortBy[ToExpression[
First[StringSplit[#, RegularExpression["\\d+?\\$"]]]] & /@
List @@ i, -Length[#] &]]], {i, EdgeList[graph]}],
EdgeLabels -> Placed["EdgeWeight", 1/4], VertexLabels -> "Name"];
path = FindShortestPath[weighGraph, people, "{}"];
HighlightGraph[graph, Subgraph[weighGraph, path],
EdgeLabels -> (Rule @@@
Transpose[{#,
Style[ToString[PropertyValue[{weighGraph, #}, EdgeWeight]],
Bold, Medium, Darker@Green, 18] & /@ #} &@
EdgeList@Subgraph[weighGraph, path]]),
VertexLabels ->
Map[Rule[#,
Style[StringReplace[
First[StringSplit[#, RegularExpression["\\d+?\\$"]]], {"{" ->
"", "}" -> ""}], Bold, Medium, Blue, 18]] &, path],
GraphHighlightStyle -> "Thick",
GraphLayout -> "LayeredDigraphEmbedding"]
As you can see,the cost time is $3 + 1 + 12 + 3 + 3 + 1 + 6=29(minute)$.
If we want to find all path,we can use FindPath to do it,and select that path shortest.
allPath =
MinimalBy[FindPath[weighGraph, people, "{}", Infinity, All],
Total[PropertyValue[{weighGraph, #}, EdgeWeight] & /@
EdgeList@Subgraph[weighGraph, #]] &];
HighlightGraph[graph, Subgraph[weighGraph, #],
EdgeLabels -> (Rule @@@
Transpose[{#,
Style[ToString[PropertyValue[{weighGraph, #}, EdgeWeight]],
Bold, Medium, Darker@Green, 18] & /@ #} &@
EdgeList@Subgraph[weighGraph, #]]),
VertexLabels ->
Map[Rule[#,
Placed[Style[
StringReplace[
First[StringSplit[#,
RegularExpression["\\d+?\\$"]]], {"{" -> "", "}" -> ""}],
Bold, Medium, Blue, 18], Center]] &, #],
GraphHighlightStyle -> "Thick",
GraphLayout -> "LayeredDigraphEmbedding",
ImageSize -> 320] & /@ allPath
As you can see,all the shortest path is $29(minute)$j,and the green number is time of every step cost.
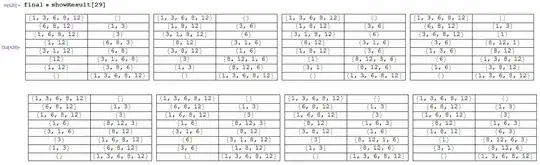
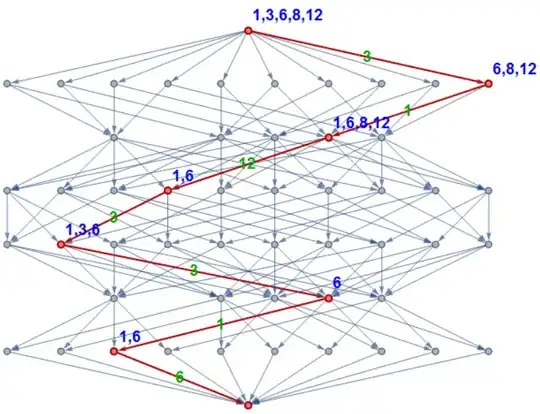
MathematicaandMathematical– yode Mar 28 '16 at 12:02Mathematicato implement it. – yode Mar 28 '16 at 13:59mmabyGraph. – yode Mar 29 '16 at 04:04