Create a square polygon that can be used as the base of a pyramid

Question

For example I want to use the design generated by this code as the base of a pyramid as well as other iterations of the design

carpet[n_] := Nest[ArrayFlatten[{{#, #, #}, {#, 0, #}, {#, #, #}}] &, 1, n]

ArrayPlot[carpet[2], PixelConstrained -> 40]

Mathematica graphics

Sounds like you're looking for Texture and VertexTextureCoordinates. Related. — Martin Ender, Mar 30 '16 at 14:12
True except I want to then 3D print this object and have the design as a physical aspect not simply a picture — ayrnee, Mar 30 '16 at 14:20
@ayrnee So, you want to generate the same patern in 3D in a pyramid or only on the base of the pyramid (not sure to understand)? — physicien, Mar 30 '16 at 14:55

Dr. belisarius · Answer 1 · 2016-03-30T17:49:12.753

Perhaps something like this:

i = ImageResize[ColorNegate@Image[carpet[2]], 300]
j = Join[{#, 0} & /@ PixelValuePositions[i, 0.], {#, 1} & /@   PixelValuePositions[i, 1.]];
g = Interpolation[j, InterpolationOrder -> 0];

RegionPlot3D[z < x + y && g[x, y] == 0, {x, 1, 300}, {y, 1, 300}, {z, 1, 300}, 
             PlotPoints -> 50, Mesh -> None]

Mathematica graphics

or perhaps

i = ImageResize[ColorNegate@Image[carpet[2]], 20];
o = Flatten /@ Tuples[{PixelValuePositions[i, 0.], Range@20}];
Graphics3D[{EdgeForm[None], (Cuboid[{##}] & @@@ o)}, Boxed -> False]

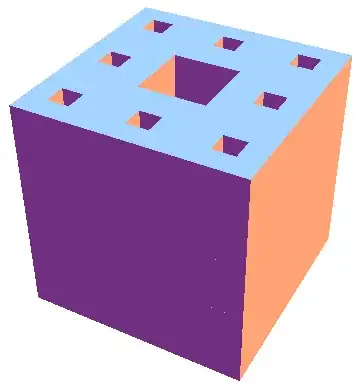
Mathematica graphics

s = 100;
i = ImageResize[ColorNegate@Image[carpet[2]], s]; 
t = Table[Thread[{Select[PixelValuePositions[i, 0.], Max[Abs[(s + 1)/2 - #] & /@ #] < j &], j}],
         {j, IntegerPart[(s + 1)/2]}];
Graphics3D[{EdgeForm[None], Cuboid @@ {#} & /@ Flatten /@ Flatten[t, 1]}]

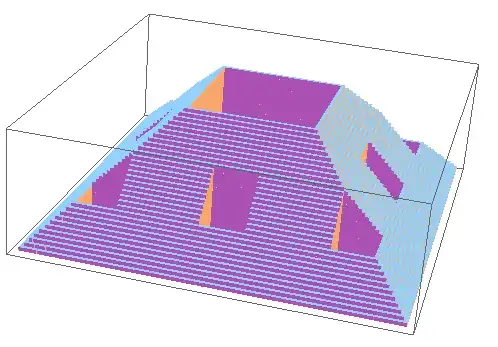
Mathematica graphics

Perhaps like the cube, but with pyramid (pyramid with holes from the base)? — physicien, Mar 30 '16 at 16:07

Michael Seifert · Accepted Answer · 2016-04-04T13:35:25.033

6

Building off of Dr. belisarius's answer: is this what you're looking for?

n = 20;
i = ImageResize[ColorNegate@Image[carpet[2]], n]
pixpos = PixelValuePositions[i, 0.];
pyramids = Pyramid[{Append[# + {1/2, 1/2}, 0], Append[# + {1/2, -1/2}, 0], 
                    Append[# + {-1/2, -1/2}, 0], Append[# + {-1/2, 1/2}, 0], 
                    {(n + 1)/2, (n + 1)/2, -n}}] & /@ pixpos;

Graphics3D[{EdgeForm[None], pyramids}]

enter image description here

There's probably a more efficient way of doing this rather than using all those Append's, but I have to run and can't improve this just now.

edited Apr 04 '16 at 13:35

answered Mar 30 '16 at 18:11

Michael Seifert

15,208
31
68

This is exactly what I am looking for but when I try to move this code into mathematica to use it I get a boatload of errors – ayrnee Apr 04 '16 at 11:32
@ayrnee: Fixed it. I should have been using Append instead of AppendTo. – Michael Seifert Apr 04 '16 at 13:35
Perfect that is so much help. But I am now having issues when I try the arguments 3,4 and 5 for carpet which I need to complete this project. For some reason they show a pyramid but without any design on the base – ayrnee Apr 04 '16 at 14:09
n represents the number of "pixels" in the base. You'll need to increase it if you want to do a higher-resolution design on the base. For carpet[3], carpet[4], and carpet[5], you'll probably want to set $n$ equal to $3^3$, $3^4$, or $3^5$ respectively. This code may start to get pretty unwieldy for the last of these. – Michael Seifert Apr 04 '16 at 14:13

score 2 · Answer 3 · answered Mar 19 '22 at 12:33

mm = MengerMesh[2];

meshcoords = Append[Append[0] /@ #, Append[1] @ Mean @ #] & @ MeshCoordinates[mm];

prims = Pyramid[Append[Length @ meshcoords] @ #] & /@ MeshCells[mm, 2][[All, 1]];

mengerPyramid = MeshRegion[meshcoords, prims, PlotTheme -> "Polygons"]

Use mm = MengerMesh[3] above to get

Create a square polygon that can be used as the base of a pyramid

3 Answers3