Solving simple transcendental equation

Question

I would like to solve

Tan[x] == 1/x

Solve[] does not work, suggesting that there is no nice analytical solution for x.

Surprisingly, NSolve[] does not work either:

NSolve[Tan[x] == 1/x, x, Reals]

returns: 'This system cannot be solved with the methods available to NSolve'

However, plotting these two functions shows that they cross around x=0.86:

This looks suspiciously close to Cos[Pi/6] = 0.866025 but it isn't. It's about 0.86028 (obtained by expanding the graph).

Am I missing something really obvious??

Thanks

There are infinitely many roots, so you need to specify the one you want: Solve[{Tan[x] == 1/x, 0 < x < 1}, x]. Alternatively, using cotSol[] from this answer: N[cotSol[1], 20]. — J. M.'s missing motivation, Mar 31 '16 at 16:48
This is a duplicate of Can Reduce really not solve for x here?. However if it doesn't enlighten you, take a look at Roots of a characteristic equation. Can Mathematica solve it?. — Artes, Mar 31 '16 at 16:51
As J.M. mentioned, there are many roots. So if you Reduce it to the area between two singularities: Reduce[Tan[x] == 1/x && 0 < x < Pi/2, Reals], you get a pure function x == Root[{-1 + #1 Tan[#1] &, 0.86033358901937976248}] — MathX, Mar 31 '16 at 16:53
Duh, yes I see. Tan(x) will cross 1/x lots of places, of course. Thanks all. — pdini, Mar 31 '16 at 17:01

score 5 · Accepted Answer · answered Mar 31 '16 at 16:48

5

Instead of finding the intersection, you can also look for the root of Tan[x]-1/x, which yields the desired result

FindRoot[Tan[x] - 1/x == 0, {x, 0.5}]
{x -> 0.860334}

Greetings, Jürgen

answered Mar 31 '16 at 16:48

user39077

66
1

Right! Yes it works, thank you. I had forgotten about that function :) – pdini Mar 31 '16 at 16:52

score 5 · Answer 2 · answered Mar 31 '16 at 16:52

NSolve is primarily meant for polynomial equations, or equations that can be transformed into a polynomial.

For equations like this, we usually have two choices:

FindRoot to find a single solution numerically, based on a starting guess
Reduce can often find an "exact" solution (in some sense), but to succeed it typically requires specifying an interval in which to look.

This equation has an infinite number of real solutions.

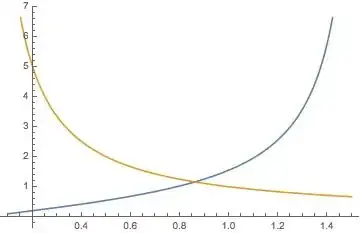
Plot[{Tan[x], 1/x}, {x, -3 Pi, 3 Pi}]

Use FindRoot to find one:

FindRoot[Tan[x] == 1/x, {x, 1}]
(* {x -> 0.860334} *)

Use Reduce to find all solutions in a given interval:

Reduce[Tan[x] == 1/x && -2 Pi < x < 2 Pi, x, Reals]

(* x == Root[{-1 + #1 Tan[#1] &, -3.4256184594817281465}] || 
 x == Root[{-1 + #1 Tan[#1] &, -0.86033358901937976248}] || 
 x == Root[{-1 + #1 Tan[#1] &, 0.86033358901937976248}] || 
 x == Root[{-1 + #1 Tan[#1] &, 3.4256184594817281465}] *)

Note that Reduce[Tan[x] == 1/x, x, Reals] does not return any solution. Specifying the interval was essential.

This latter solution is exact in the following sense:

When Reduce succeeds, it is guaranteed to find all solutions in the given interval
The Root objects, while based on a numerical approximation, represent an exact solution, and can be used as any other exact number in Mathematica (e.g. can be computed to arbitrary precision).

This interesting and useful feature of Reduce is discussed in this Wolfram Blog post.

Solving simple transcendental equation

2 Answers2