3

I'm trying to create an animation of Lorenz equation as a function of t. Here is the numerical solution of the equation:

   s = NDSolve[{x'[t] == 10 (y[t] - x[t]), 
   y'[t] == 23 x[t] - y[t] - x[t] z[t], z'[t] == x[t] y[t] - 8/7 z[t],
    x[0] == z[0] == 2, y[0] == 2}, {x, y, z}, {t, 0, 70}]

I can create a simple plot of x,y and z from t=0 to a specific t:

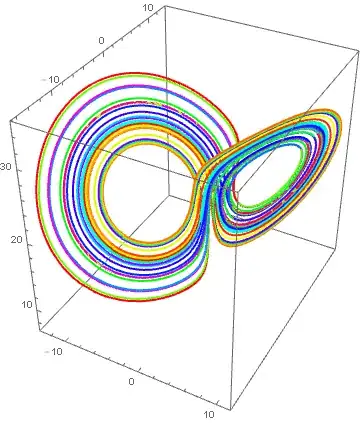
ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. s], {t, 0, 70}]

I just couldn't figure out how to create an 3D animated graph of x(t), y(t) and z(t) as a function of t.

Thanks in advance.

2 Answers2

5

To make an animation, I like to make a table of images and then animate it using ListAnimate or export an animated gif (if you want to make a quality movie, like an .avi or .mp4, then you need to export the frames and use a different program from Mathematica).

imgtable = Table[
    ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. s], {t, 0, tmax}, 
     PlotRange -> {{-14, 21}, {-17, 21}, {-1, 40}}],
    {tmax, 0.1, 70, .1}];~Monitor~tmax

ListAnimate[imgtable]

enter image description here

Jason B.
  • 68,381
  • 3
  • 139
  • 286
  • Why do the parts of the curve which are supposed to be static seem to wobble a bit? – Alexey Bobrick Apr 01 '16 at 17:46
  • @AlexeyBobrick I wish I knew. Possibly the viewpoint or angle changes, but I'm not really sure that's it at all. – Jason B. Apr 01 '16 at 20:00
  • I think I know why now. It is probably not the viewpoint, because the frame is static. It is more likely that the curve interpolation points are resampled as the span range of the parameter (tmax) changes. Resampling (remeshing) leads to small changes between the mesh points, and hence the wobbling. – Alexey Bobrick Apr 01 '16 at 21:58
1
s = NDSolve[{x'[t] == 10 (y[t] - x[t]), 
   y'[t] == 23 x[t] - y[t] - x[t] z[t], z'[t] == x[t] y[t] - 8/7 z[t],
    x[0] == z[0] == 2, y[0] == 2}, {x, y, z}, {t, 0, 70}]

ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. s], {t, 1, 70}, 
 PlotPoints -> 1000, ColorFunction -> (Hue[#4] &)]

enter image description here

Edit

With my first attempt I have overlooked "animate", sorry. As a addendum to JasonB I show a procedure with Animateand AnimateRate. 

Animate[
 ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. s], {t, 0, tend}, 
  PlotPoints -> 500, ColorFunction -> (Hue[#4] &), 
  PlotRange -> {{-15, 25}, {-20, 25}, {-2, 40}}], {tend, 0.1, 70}, 
 AnimationRate -> 1.5]

enter image description here