Animate spherical pendulum

Question

I want to plot the position of Spherical pendulum.

First I tried to plot the simple pendulum:

DSolve[{y''[t] == -y[t], y[0] == Pi/2, y'[0] == 0}, y[t], t]
(* {{y[t] -> 1/2 Pi Cos[t]}} *)

then manipulate $t$

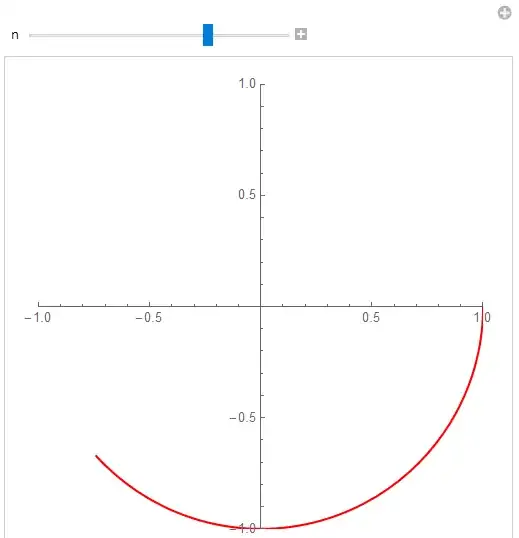
Manipulate[
ParametricPlot[{Sin[ 1/2 Pi Cos[t]], -Cos[1/2 Pi Cos[t]]}, {t, 0, n},
    PlotRange -> 1,PlotStyle -> Red], {n, 0.1, 2Pi, 0.01}]

I want to do same thing for spherical pendulum.

These are differential equations of the spherical pendulum page,3

sys := {θ''[t] == ϕ'[t]^2 Cos[θ[t]] - g/l Sin[θ[t]], ϕ''[t] == 
    (-2 ϕ'[t] θ'[t] Cos[θ[t]])/Sin[θ[t]]}

with initial condition

ic := {θ[0] == π/2, θ'[0] == 0, ϕ[0] == π/2, ϕ'[0] == 1}

I tried:

sol = NDSolve[{θ''[t] == ϕ'[t]^2 Cos[θ[t]] - g/l Sin[θ[t]], 
    ϕ''[t] == (-2 ϕ'[t] θ'[t] Cos[θ[t]])/Sin[θ[t]], θ[0] == π/2, 
    θ'[0] == 0, ϕ[0] == π/2, ϕ'[0] == 1} /. {g -> 9.81, l -> 1}, {θ, ϕ}, {t, 0, 10}] 
x[t_] := Evaluate[(Sin[θ[t]] Cos[ϕ[t]]) /. sol] 
y[t_] := Evaluate[(Sin[θ[t]] Sin[ϕ[t]]) /. sol]
z[t_] := Evaluate[Cos[θ] /. sol]

ParametricPlot3D[{x[t], y[t], z[t]}, {θ, 0, 2 π}, {ϕ, -π, π}]

but it doesn't work

There are several demos for this on the Wolfram site, see e.g. here — Jens, Apr 02 '16 at 19:50
Given the age of this post, I think this should be closed as a duplicate of Animation of double pendulum because it's kind of a special case of that question, at least as far as MMA aspects are concerned. The actual issue here is too localized. — Jens, Aug 05 '18 at 17:16

bbgodfrey · Answer 1 · 2016-04-02T14:33:47.570

A few changes give the desired result.

sol = Flatten@
    NDSolve[{θ''[t] == ϕ'[t]^2 Cos[θ[t]] - g/l Sin[θ[t]], ϕ''[t] == 
    (-2 ϕ'[t] θ'[t] Cos[θ[t]])/Sin[θ[t]], θ[0] == π/2, θ'[0] == 0, 
    ϕ[0] == π/2, ϕ'[0] == 1} /. {g -> 9.81, l -> 1}, {θ, ϕ}, {t, 0, 10}] 
x[t_] := Evaluate[(Sin[θ[t]] Cos[ϕ[t]]) /. sol] 
y[t_] := Evaluate[(Sin[θ[t]] Sin[ϕ[t]]) /. sol] 
z[t_] := Evaluate[Cos[θ[t]] /. sol] 
ParametricPlot3D[{x[t], y[t], z[t]}, {t, 0, 10}]

By the way, replacing the last four lines by

ParametricPlot3D[{Sin[θ[t]] Cos[ϕ[t]], Sin[θ[t]] Sin[ϕ[t]], Cos[θ[t]]} /. sol, {t, 0, 10}]

is a bit simpler. Also, there is no need to use SetDelayed to define sys and ic. Use Set instead.

Animate spherical pendulum

1 Answers1