Image of the unit circle under a complex rational function

Question

Let $$f(z)=\dfrac{z(z-a)}{(z-b)(z-c)(z-d)}$$ be a complex rational function with distinct non zero complex numbers $a,b,c$ and $d.$

I need to plot the image of the unit circle $S=\{z\in\mathbb{C} : |z|=1\}$ under $f$ and compare it with $S$ by varying $a,b,c$ and $d.$

How can I do this?

Closely related Plotting complex numbers as an Argand Diagram. If it is not a duplicate, explain why. — Artes, Apr 06 '16 at 06:33
@Artes: Closely related does not means that this is a duplicate. — Bumblebee, Dec 26 '16 at 18:57

score 4 · Accepted Answer · answered Apr 21 '16 at 22:10

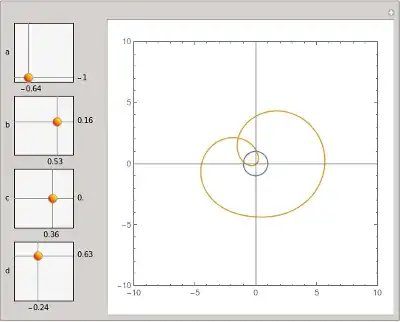
Generate complex points cc on the unit circle, then map them with your function $f(z)$. Plot the unit circle and its image together, while manipulating the four parameters.

With[{cc = CirclePoints[1000.].{1, I}},
   Manipulate[
      ListLinePlot[
         {ReIm[cc],
          ReIm[cc*(cc - a.{1,I})/((cc - b.{1,I})*(cc - c.{1,I})*(cc - d.{1,I}))]
         },
         PlotRange -> 10*{{-1,1},{-1,1}}, Frame -> True, AspectRatio -> Automatic
      ],
      {{a, {0, 0}}, {-1, -1}, {1, 1}, Appearance -> "Labeled"},
      {{b, {0, 0}}, {-1, -1}, {1, 1}, Appearance -> "Labeled"},
      {{c, {0, 0}}, {-1, -1}, {1, 1}, Appearance -> "Labeled"},
      {{d, {0, 0}}, {-1, -1}, {1, 1}, Appearance -> "Labeled"},
      ControlPlacement -> Left
   ]]

Image of the unit circle under a complex rational function

1 Answers1