MeshCoordinates from a RegionBoundary no longer in proper order in version 10.4

Question

Bug introduced in V10.4 and persists through 10.4.1

Given that I have the following data set

mat = 
 {{{0.,-5.,0.},{-5.22027,0.,1.79454}},
 {{-0.858274,-4.93844,0.0924},{-5.41893,0.782172,1.77784}}, 
 {{-1.82027,-4.75528,-0.109357},{-5.60223,1.54509,1.95084}},
 {{-2.94275,-4.45503,-0.550252},{-5.77547,2.26995,2.3602}},
 {{-4.31974,-4.04509,-1.18618},{-5.94562,2.93893,3.03783}},
 {{-6.12372,-3.53553,-2.00001},{-6.12372,3.53553,3.99999}}};

domain = 
  {{{5.0165, 2 Pi}, {0, 0.756304}}, {{3.4076, 2 Pi}, {0, 2.31521}}, 
   {{3.7396, 2 Pi}, {0, 1.93244}}, {{3.85122, 2 Pi}, {0, 1.86739}},  
   {{3.91005, 2 Pi}, {0, 1.87528}}, {{3.94139, 2 Pi}, {0, 1.91028}}};

ellipsePoints[mat_, {x_, y_}] := 
  mat.{Sin[#], Cos[#], 1} & /@ Range[x, y, 0.02 Pi]
ellipsePoints[mat_, {{a_, b_}, {c_, d_}}] := 
  mat.{Sin[#], Cos[#], 1} & /@ 
   Join[Range[a, b, 0.02 Pi], Range[c, d, 0.02 Pi]]

pts = Flatten[MapThread[ellipsePoints, {mat, domain}], 1];

With help of RunnyKine's alphaShapes2DC[] function, I can find the approximate boundary

Show[Graphics[Point[pts]], RegionBoundary@alphaShapes2DC[pts, 5.5]]

enter image description here

However, when I get the coordinates of the boundary via MeshCoordinates[], which gives me a wrong order of point-set.

ListLinePlot@MeshCoordinates@RegionBoundary@alphaShapes2DC[pts, 5.5]

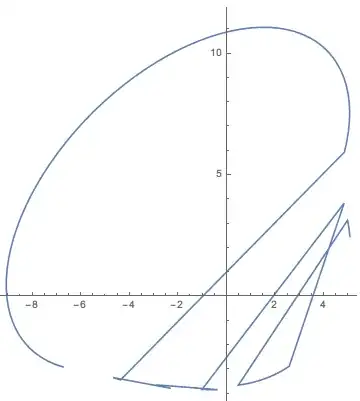
enter image description here

So my question is:(I using the Mathematica V$10.4$ on Windows $32$ bit system)

How to do to achieve the right order of point-set?

What version are you using? When I run that last line I get the correct result: http://i.stack.imgur.com/tfiZM.png — Jason B., Apr 06 '16 at 09:37
@JasonB I using the Mathematica V$10.4$ on Windows 32 bit system. — xyz, Apr 06 '16 at 09:42
I can verify that this works great on 10.0 through 10.3.1, but not 10.4 — Jason B., Apr 06 '16 at 09:57
@JasonB OK, thansks for your testing:) It should be a bug introduced in the latest version $10.4$. — xyz, Apr 06 '16 at 10:26
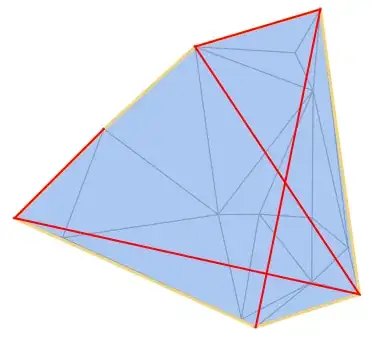
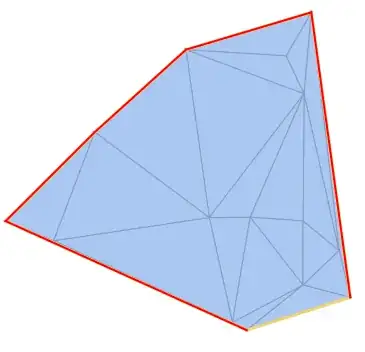
Yeah, I'm working on a workaround right now. I could reformulate the question to be easy for others to verify, as in it doesn't need to even refer to alphapoints function, it applies to any BoundaryMeshRegion. — Jason B., Apr 06 '16 at 10:27
@JasonB I tried the FindCurvePath[] just now, but this built-in failed to find the continuous curve. — xyz, Apr 06 '16 at 10:43

score 2 · Accepted Answer · edited Apr 06 '16 at 11:56

Let's look at a simpler example to show the problem. We'll create a Delaunay mesh from some random points, and generate a RegionBoundary from that.

In version 10.4:

SeedRandom[4];
mr1 = DelaunayMesh[RandomReal[1, {15, 2}]];
mr2 = RegionBoundary[mr1];
Show[mr1, HighlightMesh[mr2, 1], 
 ListLinePlot[MeshCoordinates@mr2, 
  PlotStyle -> Directive[Thick, Red]]]

compared with version 10.3.1 (or any previous version 10.x)

Let's look at the InputForm for this in 10.4,

mr2 // InputForm


MeshRegion[{.....}, {Line[{{2, 6}, {1, 2}, {4, 1}, {3, 5}, {6, 3}, {5, 4}}]}]

versus for 10.3,

MeshRegion[{.....}, {Line[{{1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 6}, {6,1}}]}]

How to get around this? Create a BoundaryMeshRegion and extract the polygon points from that (the points of a polygon must be in the right order or it's nonsense). The following gives identical results in 10.3 and 10.4

SeedRandom[4];
mr1 = DelaunayMesh[RandomReal[1, {15, 2}]];
mr2 = BoundaryDiscretizeRegion[mr1];
Show[mr1, HighlightMesh[mr2, 1], 
 ListLinePlot[First@First@MeshPrimitives[mr2, 2], 
  PlotStyle -> Directive[Thick, Red]]]

And, applied to the OP,

ListLinePlot@First@First@MeshPrimitives[#, 2] &@
 BoundaryDiscretizeRegion@alphaShapes2DC[pts, 5.5]

So the algorithm has changed in V$10.4$. – xyz Apr 06 '16 at 11:13 — xyz, Apr 06 '16 at 11:13

MeshCoordinates from a RegionBoundary no longer in proper order in version 10.4

1 Answers1

Linked