How to convert a graph to a mesh region

Question

As we know,the region is very convenient in Mathematica.And we can convert a MeshRegion into graph like this

SeedRandom[7]
pts = RandomReal[1, {5, 2}];
voronoi = VoronoiMesh[pts]

gvoronoi = 
 AdjacencyGraph[voronoi["AdjacencyMatrix"], 
  VertexCoordinates -> MeshCoordinates[voronoi]]

But the question is how to convert the graph name as gvoronoi back into voronoi?I can convert it into a 1-dimension region like this

DiscretizeGraphics[
 Graphics@GraphicsComplex[GraphEmbedding[gvoronoi], 
   Line[List @@@ EdgeRules@gvoronoi]]]

But we target is convert it back into a exact voronoi.How to do this?

Answer 1

Below you'll find the method I wrote myself, but it is terribly slow compared to this one, adapted from halmir's code here, so I will give the fast version first and post my own code below. See halmir's post for an explanation,

ClearAll@graphToMesh
graphToMesh[graph_?PlanarGraphQ] := 
 Module[{nextCandidate, m, orderings, pAdj, rightF, s, t, initial, 
   face, emb, faces},
  emb = GraphEmbedding[graph];
  nextCandidate[ss_, tt_, adj_] := Module[{length, pos},
    length = Length[adj];
    pos = Mod[Position[adj, ss][[1, 1]] + 1, length, 1];
    {tt, adj[[pos]]}];
  m = AdjacencyMatrix[graph];
  Do[pAdj[v] = 
    SortBy[Pick[VertexList[graph], m[[v]], 1], 
     ArcTan @@ (emb[[v]] - emb[[#]]) &], {v, VertexList[graph]}];
  rightF[_] := False;
  faces = Reap[Table[If[! rightF[e], s = e[[1]];
       t = e[[2]];
       initial = s;
       face = {s};
       While[t =!= initial, 
        rightF[UndirectedEdge[s, t]] = True;
        {s, t} = nextCandidate[s, t, pAdj[t]];
        face = Join[face, {s}];];
       Sow[face];],
      {e, EdgeList[graph]}]][[2, 1]];
  faces = Most[SortBy[faces, Area[Polygon[emb[[#]]]] &]];
  MeshRegion[emb, Polygon[faces]]
  ]

Applied to the original graph,

graphToMesh[gvoronoi]

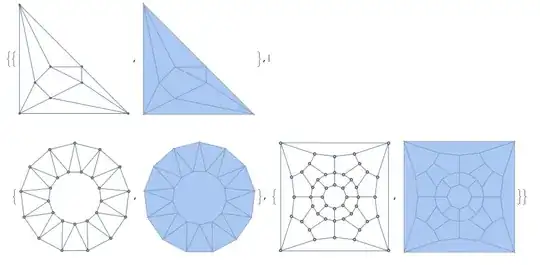
These examples all run pretty quickly,

{#, graphToMesh[#]} & /@ {HararyGraph[4, 8, 
   GraphLayout -> "PlanarLayout"], GraphData[{"Antiprism", 13}], 
  GraphData["ZamfirescuGraph48"]}

Old, slower answer based on RegionIntersection

The previous answer I had posted seemed to work for any mesh region created from a VoronoiMesh but would fail for other types of graphs. This method is slower but more robust. It seeks to the minimal basis of non-overlapping regions in a graph, using the function graphToFaces described here

graphToFaces[graph_?PlanarGraphQ] := Module[{graphpoints, cycles, polygons, n},
  graphpoints = GraphEmbedding[graph];
  cycles = 
   Polygon[graphpoints[[#]]] & /@ 
    FindCycle[graph, Infinity, All][[All, All, 2]];
  cycles = SortBy[cycles, Area];
  polygons = {cycles[[1]]};
  n = 2;
  While[Length@polygons < Length@FindFundamentalCycles@graph && 
    n <= Length@cycles,
   If[
    And @@ (Area[RegionIntersection[cycles[[n]], #]] === 0 & /@ 
       polygons),
    AppendTo[polygons, cycles[[n]]]
    ];
   n++
   ];
  First /@ (polygons /. Thread[graphpoints -> Range@Length@graphpoints])
  ]

graphToMesh[graph_?PlanarGraphQ] := 
 MeshRegion[GraphEmbedding[graph], Polygon[graphToFaces[graph]]]

Here it is applied to six random Voronoi mesh objects,

Table[pts = RandomReal[1, {5, 2}];
 voronoi = VoronoiMesh[pts];
 gvoronoi = 
  AdjacencyGraph[voronoi["AdjacencyMatrix"], 
   VertexCoordinates -> MeshCoordinates[voronoi]];
 {voronoi, graphToMesh[gvoronoi]}, {6}]

In each result above, the output is identical to the input mesh.