How to pick out the element in a list of lists which satisfies a particular condition?

Question

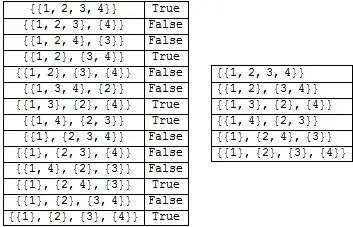
I have got a list:

lis:={
{{1, 2, 3, 4}},
{{1, 2, 3}, {4}},
{{1, 2, 4}, {3}},
{{1, 2}, {3, 4}},
{{1, 2}, {3}, {4}},
{{1, 3, 4}, {2}},
{{1, 3}, {2}, {4}},
{{1, 4}, {2, 3}},
{{1}, {2, 3, 4}},
{{1}, {2, 3}, {4}},
{{1, 4}, {2}, {3}},
{{1}, {2, 4}, {3}},
{{1}, {2}, {3, 4}},
{{1}, {2}, {3}, {4}}
};

and I would like to pick out those lists which satisfy the following condition:

list == Mod[list+2,4,1]

but, they should be "equal" as a set of lists, not in a "element to element" way. For example, {{1,2},{3,4}} is a list satisfied the condition, since Mod[{{1,2},{3,4}}+2,4,1] is {{3, 4}, {1, 2}}, which is not equal to {{1,2},{3,4}} since the "position" is not right, but we should regard it as equal in the sense of set, since they are both the set of {1,2} and {3,4}.

An example which not satisfied our condition is that {{1,2,3},4}, since Mod[{{1, 2, 3}, 4} + 2, 4, 1] is {{3, 4, 1}, 2}, as a set they are not equal, one is the union of {1,2,3} and {4}, but the results is the union of {1,3,4} and {2}.

Can I use a pattern to sort out the one satisfied my condition in the list? I would like to make it work with any list.

score 7 · Answer 1 · edited Jan 27 '20 at 14:06

A more mathematically intuitive formulation would be to use Intersection, as then the logic is self-explanatory. You can also create a custom container to make the sets orderless so that {1,2,3}, {3,1,2} and {2,3,1} are all treated the same (alternately, you can use Sort). For example:

equivalentQ[func_] := Block[{f},
    SetAttributes[f, Orderless];
    With[{set = # /. List -> f}, 
        Intersection[set, func@# /. List -> f] === set
    ]
] &;

Sets that equal those transformed by func should yield True. With this, you can write your condition as

 cond = equivalentQ[Mod[# + 2, 4, 1] &]

(and easily extend it to other transformation functions).

Select:

Select[list, cond]
(* {{{1, 2, 3, 4}}, {{1, 2}, {3, 4}}, {{1, 3}, {2}, {4}}, 
    {{1, 4}, {2, 3}}, {{1}, {2, 4}, {3}}, {{1}, {2}, {3}, {4}}} *)

Cases:
```
Cases[list, x_List /; cond[x]]
```
Pick:
```
Pick[list, cond /@ list]
```

Reap & Sow:

Last@Reap@Scan[If[cond[#], Sow[#]] &, list]

score 4 · Accepted Answer · answered Sep 28 '12 at 15:00

4

If my reading of your question is correct, this does the job:

sets = {{{1, 2, 3, 4}}, {{1, 2, 3}, {4}}, {{1, 2, 4}, {3}}, {{1, 2}, {3, 4}},
        {{1, 2}, {3}, {4}}, {{1, 3, 4}, {2}}, {{1, 3}, {2}, {4}},
        {{1, 4}, {2, 3}}, {{1}, {2, 3, 4}}, {{1}, {2, 3}, {4}},
        {{1, 4}, {2}, {3}}, {{1}, {2, 4}, {3}}, {{1}, {2}, {3, 4}},
        {{1}, {2}, {3}, {4}}};

Cases[sets, list_List /; Equal @@ Map[Sort, {list, Mod[list + 2, 4, 1]}, 2]]
   {{{1, 2, 3, 4}}, {{1, 2}, {3, 4}}, {{1, 3}, {2}, {4}},
    {{1, 4}, {2, 3}}, {{1}, {2, 4}, {3}}, {{1}, {2}, {3}, {4}}}

answered Sep 28 '12 at 15:00

J. M.'s missing motivation

124,525
11
401
574

yes, it seems you were right, thanks! but could you please explain the code for me? why it works? – van abel Sep 28 '12 at 15:07
The condition I used within Cases[] can be written in an equivalent, longer, but maybe more transparent form: Sort[Map[Sort, list]] == Sort[Map[Sort, Mod[list + 2, 4, 1]]]. I trust that this form might be more understandable to you. The key is in the third argument of Map[]; see the docs for details. – J. M.'s missing motivation Sep 28 '12 at 15:14
you means that the argument 2 of map means to sort the two list in the list {list, mod...}(whose element are numbers), not to sort the whole list (whose elements are lists)? – van abel Sep 28 '12 at 15:40
If you're doubting how something like Map[] works here, it is instructive to replace the Sort[] with a "generic" function. Try Remove[f]; With[{l = {{1}, {2}, {3, 4}}}, Map[f, {l, Mod[l + 2, 4, 1]}, 2]]. – J. M.'s missing motivation Sep 28 '12 at 15:43
ok, good demo. thanks! – van abel Sep 28 '12 at 23:55

Mr.Wizard · Answer 3 · 2012-09-29T06:42:32.193

3

I failed to spell out a working solution for your problem the first time. Here is what I intended:

sortall = # /. List :> Composition[Sort, List]&;

Select[lis, sortall @ #  === sortall @ Mod[# + 2, 4, 1] &]

{{{1, 2, 3, 4}}, {{1, 2}, {3, 4}}, {{1, 3}, {2}, {4}},
 {{1, 4}, {2, 3}}, {{1}, {2, 4}, {3}}, {{1}, {2}, {3}, {4}}}

J.M.'s method is cleaner, and in this case without a downside that I can see. (The sortall function is useful if you want to sorts Lists and only Lists at any level in an expression.) I still prefer Select here:

Select[lis, Equal @@ Map[Sort, {#, Mod[# + 2, 4, 1]}, 2] &]

edited Sep 29 '12 at 06:42

answered Sep 28 '12 at 14:18

Mr.Wizard

271,378
34
587
1,371

1

they are both not work for the lis={{1, 5, 6}, {2, 3, 4}}. – van abel Sep 28 '12 at 14:55
@vanabel please explain in detail how that set passes your test. – Mr.Wizard Sep 28 '12 at 14:58
1

(Mod[# + 6/2, 6, 1] /. List :> Composition[Sort, List]) & /@ lis will output {{2, 3, 4}, {1, 5, 6}}, which is not equal to {{1,5,6},{2,3,4}} as a "list". – van abel Sep 28 '12 at 15:00
1

Both versions miss the lists with a mix of singletons and longer lists, like {{1, 3}, {2}, {4}}. To fix the first one: Select[lis, Sort[Sort /@ #] === Sort[Sort /@ Mod[# + 2, 4, 1]] &] – J. M.'s missing motivation Sep 28 '12 at 15:47

score 3 · Answer 4 · answered Sep 28 '12 at 20:49

3

Along the same lines as @R.M.'s approach:

eqvlntQ = Union[Union /@ #] == Union[Union /@ Mod[# + 2, 4, 1]] &;

which can be used with Pick, Select, Cases and Reap/Sow as in @R.M's answer.

Row[{{#, eqvlntQ[#]} & /@ sets // Grid[#, Frame -> All] &, 
 Pick[sets, eqvlntQ /@ sets] // Column[#, Frame -> All] &}, Spacer[10]]

enter image description here

answered Sep 28 '12 at 20:49

kglr

394,356
18
477
896

yes, you were right: since Union has the function of sort as mentioned the doc
Union[list_1,list_2],...] gives a sorted list of all the distinct elements that appear in any of the list_i.
– van abel Sep 29 '12 at 00:11

How to pick out the element in a list of lists which satisfies a particular condition?

4 Answers4

Linked