I have two equations:
{2 x + y + z == 1, 3 x - 2 y - z == 5}
And I have calculated the answers on paper, which gave me $x = 1 + t$, $y = -1 + 5t$ and $z = -7t$.
So my actual problem is how I should do this with Mathematica. I haven't really worked with Mathematica that much, and therefore I don't know how I should get these answers, and also plot the intersection of these two planes.
I would appreciate it if someone could guide me or show me some way to do it.
Just to illustrate some other things. You can which parametrization you like. In this case parametrization in terms of x:
sol = {x, y, z} /. First@Solve[eq, {y, z}];
Show[Plot3D[{1 - 2 x - y, 3 x - 2 y - 5}, {x, -2, 2}, {y, -2, 2},
Mesh -> False, PlotStyle -> {LightBlue, LightYellow}],
ParametricPlot3D[sol, {x, -2, 2}, PlotStyle -> Red,
PlotLegends ->
Column[{SwatchLegend[{LightBlue, LightYellow}, eq],
LineLegend[{Red}, {"Parametrization: " <> ToString@sol}]}]]]
You could use
sol = Solve[{2 x + y + z == 1, 3 x - 2 y - z == 5}, {x, y}] // Simplify
giving
Out[1] {{x->1-z/7,y->-((5 z)/7)-1}}
This gives x, y in terms of z. To parameterize in terms of t do
sol /. z -> -7 t
giving
Out[2] {{x->t+1,y->5 t-1}}
and of course z->-7 t
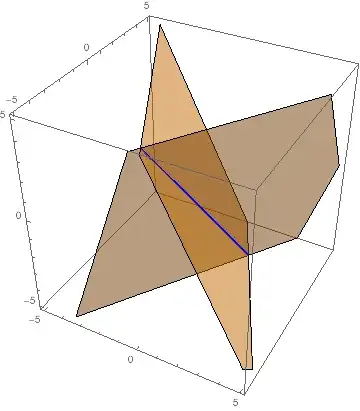
This may be overkill, but I think it is interesting to use RegionIntersection here.
plane1 =
InfinitePlane[{x, y, z} /.
FindInstance[
2 x + y + z == 1 && {x, y} ∈ Rectangle[], {x, y, z},
Reals, 3]]
plane2 = InfinitePlane[{x, y, z} /.
FindInstance[
3 x - 2 y - z == 5 && {x, y} ∈ Rectangle[], {x, y, z},
Reals, 3]]
line = RegionIntersection[
plane1, plane2
]
Graphics3D[{Red, plane1, plane2, Blue, line}]
(* InfinitePlane[{{31/302, 1, -(31/151)}, {1, 1, -2}, {33/302, 0, 118/151}}] *)
(* InfinitePlane[{{31/302, 1, -(2021/302)}, {1, 1, -4}, {33/302, 0, -(1411/302)}}] *)
(* InfiniteLine[{7/5, 1, -(14/5)}, {-(1/5), -1, 7/5}] *)
Now you have your line as an InfiniteLine object, you can convert this to a parametric form via the formulas here.
{point, vector} = List @@ line;
equation = point + vector t
(* {7/5 - t/5, 1 - t, -(14/5) + (7 t)/5} *)
Which I can show graphically is equivalent to the form OP seeks,
ParametricPlot3D[{
equation,
{1 + t, 5 t - 1, -7 t}
}, {t, 0, 5}]
Two planes always intersect in a line as long as they are not parallel. See also Plane-Plane Intersection.
You can plot two planes with ContourPlot3D,
h = (2 x + y + z) - 1
g = (3 x - 2 y - z) - 5
ContourPlot3D[{h == 0, g == 0}, {x, -5, 5}, {y, -5, 5}, {z, -5, 5}]
And the Intersection as a Mesh Function,
ContourPlot3D[{h == 0, g == 0}
, {x, -5, 5}, {y, -5, 5}, {z, -5, 5}
, MeshFunctions -> {Function[{x, y, z, f}, h - g]}
, MeshStyle -> {{Thick, Blue}}, Mesh -> {{0}}
, ContourStyle -> Directive[Orange
, Opacity[0.5], Specularity[White, 30]]]
See MeshFunctions and Function.
I'll just leave the following simple code for computing the direction numbers of a line given its two generating planes:
eqs = {2 x + y + z == 1, 3 x - 2 y - z == 5};
coefs = Normal[Last[CoefficientArrays[eqs, {x, y, z}]]];
dn = RotateLeft[Det /@ First[Partition[coefs, {2, 2}, {2, 1}, 1]]]
{1, 5, -7}
Then, just generate some point on the line; e.g.
p0 = {x, y, z} /. First[FindInstance[eqs, {z, y, x}]]
{1, -1, 0}
and one can now either use the parametric equations p0 + t dn for computations or plotting, or use InfiniteLine[p0, dn] for visualization.
The two-points-determine-a-line method:
eqs = {2 x + y + z == 1, 3 x - 2 y - z == 5};
Replace[
{x, y, z} /. FindInstance[eqs, {x, y, z}, Reals, 2],
{p_, q_} :> p + t (q - p)]
(* {1/2 + t/10, -(7/2) + t/2, 7/2 - (7 t)/10} *)
With rational equations, we can look for integral solutions:
param = Replace[
{x, y, z} /. FindInstance[eqs, {x, y, z}, Integers, 2],
{p_, q_} :> p + t (q - p)]
(* {5 + t, 19 + 5 t, -28 - 7 t} *)
We can find an integral point closest to the origin for slightly simpler parametric coordinates:
param /. t ->
t + ArgMin[#.# &@{5 + t, 19 + 5 t, -28 - 7 t}, t,
Integers] // Simplify
(* {1 + t, -1 + 5 t, -7 t} *)
