Why is this list not a valid vector field dataset or a valid list of datasets?

Question

a = 0.1
x = Pi/2
data = Table[With[{y = -1 + 0.5*i, z = -1 +0.5*j}, 
  {{NIntegrate[-(z/(t^2 - 2 t x + x^2 + y^2 + z^2)^(3/2)) 
    - (3 (y z Sin[t]) a)/(t^2 - 2 t x + x^2 + y^2 + z^2)^(
    5/2) + (3 z (t^2 - 2 t x + x^2 - 4 y^2 + z^2) Sin[t]^2 a^2)/ 
     (2 (t^2 - 2 t x + x^2 + y^2 + z^2)^(7/2)), {t, -∞, ∞}, 
   Method -> {"GlobalAdaptive", "MaxErrorIncreases" -> 200, 
     Method -> "GaussKronrodRule"}, AccuracyGoal -> 20, 
   MaxRecursion -> 20], 
  NIntegrate[y/(t^2 - 2 t x + x^2 + y^2 + z^2)^(3/2) 
   + ((t Cos[t] - x Cos[t] - Sin[t])/(t^2 - 2 t x + x^2 + y^2 + z^2)^(3/2)
      + (3 y^2 Sin[t])/(t^2 - 2 t x + x^2 + y^2 + z^2)^(5/2)) a + 
       ((3 y (t Cos[t] - x Cos[t] - Sin[t]) Sin[t])/(t^2 - 2 t x + 
         x^2 + y^2 + z^2)^(5/2) + (3 y (-t^2 + 2 t x - x^2 + 4 y^2 - z^2) Sin[t]^2)/
    (2 (t^2 - 2 t x + x^2 + y^2 + z^2)^( 7/2))) a^2, {t, -∞, ∞}, 
   Method -> {"GlobalAdaptive", "MaxErrorIncreases" -> 700, 
     Method -> "GaussKronrodRule"}, AccuracyGoal -> 20, 
   MaxRecursion -> 60] },
   0.}], {i, 0, 4}, {j, 0, 4}];

a)

data5 = data /. {_Complex -> 0.}
data1 = Flatten[data /. {_Complex -> 0.}, 1]

By = data1[[All, 1, 1]]

Bz = data1[[All, 1, 2]]

B = Sqrt[By^2 + Bz^2]

data2 = Transpose[{By, Bz}]

data3 = Transpose[{data2, B}]

data4 = {data3}

/a)

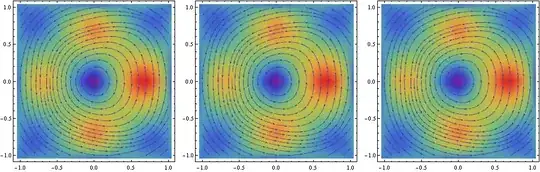
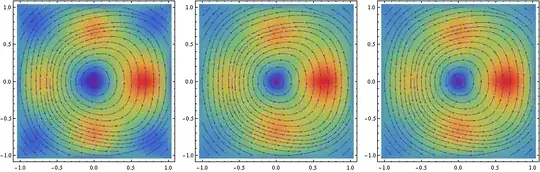
 ListStreamDensityPlot[data4, VectorScale -> Automatic, 
 Evaluated -> True, DataRange -> {{-1, 1}, {-1, 1}}, 
 ColorFunction -> ColorData["Rainbow"]

ListStreamDensityPlot::vfldata: {{{1.00103,-0.998971},1.41421},
{{0.80244,-1.60145},1.79124},{{0.,-2.00492},2.00492},{{-0.80244,-1.60145},1.79124}, 
{{-1.00103,-0.998971},1.41421},<<15>>,{{1.00103,0.998971},1.41421},
{{0.80244,1.60145},1.79124},{{0.,2.00492},2.00492},{{-0.80244,1.60145},1.79124},
{{-1.00103,0.998971},1.41421}} is not a valid vector field dataset or a valid list of 
datasets. >>

I plot with the function Edit: illustrating additional options but I didn't want to include the whole code here so the upper one is snipped. The post is already long enough but if you want I could add it.

These additional errors appears when plotting with the whole function.

FindDivisions::fdargs: "The arguments in Developer`FindDivisions[{∞,-
∞,0.5}, 10, 10] are not supported."
∞::indet: "Indeterminate expression 0\ (-∞) encountered."
∞::indet: "Indeterminate expression -∞+∞ encountered." 

I don't understand where I get ∞. I put the complex element to 0. If you check the output there is no ∞ value. That could happen because of the error "is not a valid vector field dataset or a valid list of datasets."

When I compare data5 and data4 I see no differences in format output. It works with data5 and not with data4.

The code between a) was done that way so I could plot {{By,Bz}, Norm[By,Bz]}. I couldn't find a better way.

Thanks in advance.

Answer 1

If you partition data4 you get an array with the same structure as data5. However, you can also produce the same final array in one step from data5 (examples: dataXb and dataXc below).

dataXa = Partition[data4[[1]], 5];
dataXb = data5 /. {{x_, y_}, 0.} :> {{x, y}, Norm[{x, y}]};
dataXc = {#, Norm[#]} & /@ # & /@ (First /@ # & /@ data5);
dataXa == dataXb == dataXc;
(*True *)

options = Sequence[VectorScale -> Automatic, Evaluated -> True,ImageSize -> 300,
    DataRange -> {{-1, 1}, {-1, 1}},  ColorFunction -> ColorData["Rainbow"]];
Row[ListStreamDensityPlot[#, options] & /@ {dataXa, dataXb, dataXc}, Spacer[5]]

EDIT: From ListStreamPlot >> More Information:

If no scalar field values are given, they are taken to be the norm of the vector field.

So an alternative approach is to simply remove the scalar field values to turn element {{x,y},0.} to {x,y} in data5. This can be done in a number of ways. For example:

dataXb2 = data5 /. {{x_, y_}, 0.} :> {x, y};
dataXb3 = First /@ # & /@ data5;
Row[ListStreamDensityPlot[#, options] & /@ {dataXb, dataXb2, dataXb3},Spacer[5]]