How to create a surface mesh embedded in 3D?

Question

I am working on a problem where I want to optimize current densities on 2D surfaces embedded in 3D to generate magnetic fields. The current density on a surface can be written as a scalar function multiplied by the curl of the normal vector to the surface.

Ideally, my problem could be solved in the following steps:

Create surfaces, probably as boundaries of regions in 3D
Generate a mesh on these surfaces
Optimize function values on the nodes (I know how to do this step)
Create a contour plot of this function on these surfaces (these contours are basically the wire patterns I am aiming for)

My question is about generating the surfaces, meshing them, and plotting the scalar function.

I've tried to come up with a simple example. Consider the following region:

Needs["NDSolve`FEM`"]
rI = 1/2; rA = 1;
reg = RegionProduct[Annulus[{0, 0}, {rI, rA}, {0, Pi/2}], Line[{{0}, {1}}]]

My first problem: The default boundary mesh does not reproduce the region too well, compared to a BoundaryMeshRegion:

bdm = ToBoundaryMesh[reg];
bdr = BoundaryDiscretizeRegion[reg, MaxCellMeasure -> {"Length" -> .15}];
GraphicsRow[{bdm["Wireframe"], bdr}, ImageSize -> Large]

So, I continue with the BoundaryMeshRegion. Since not all surfaces of my initial region reg will carry a current, I manually select one:

points = MeshCells[bdr, 0] /. Point[arg_] :> arg;
lines = MeshCells[bdr, 1] /. Line[arg_] :> arg;
elements = MeshCells[bdr, 2] /. Polygon[arg_] :> arg;
coords = MeshCoordinates[bdr];

radii=coords/.{x_,y_,z_}:>Sqrt[x^2+y^2];
selector[l_List]:=TrueQ[And@@((Abs[#-1.0]<10^-8)&/@radii[[l]])]
selectedPoints=Union[Flatten[Cases[elements,l_List/;selector[l],1]]];
selectedElements=Cases[elements,l_List/;selector[l],1];
selectedCoordinates=coords[[selectedPoints]];
newIndices=Thread[selectedPoints->Range[Length[selectedPoints]]];
(* Reverse is needed to get the incidents in counterclockwise order *)
newElements=Map[Reverse,selectedElements/.newIndices];
newCoords=selectedCoordinates/.{x_Real,y_Real,z_Real}:>{z,ArcTan[x,y]/(Pi/2)};

Plotting everything shows a reasonable structure, with some low quality elements:

Graphics[{
  FaceForm[], EdgeForm[LightRed],
  Polygon[newElements /. i_Integer :> newCoords[[i]]],
  Blue, Text[#, newCoords[[#]]] & /@ Range[Length[newCoords]],
  Black, Text[#, 
     Mean[newElements[[#]] /. i_Integer :> newCoords[[i]]]] & /@ 
   Range[Length[newElements]]
  }, Frame -> True]

Now I convert my manually extracted mesh back to an element mesh:

em1 = ToElementMesh[
  "Coordinates" -> newCoords,
  "MeshElements" -> {TriangleElement[newElements]}
  ];

and generate some function values:

data1 = em1["Coordinates"] /. {z_Real, u_Real} :> Sin[z Pi] Sin[u Pi];
if1 = ElementMeshInterpolation[{em1}, data1, 
  "ExtrapolationHandler" -> {Function[Indeterminate], 
    "WarningMessage" -> False}]

With this poor mesh resolution, the plot is jagged, but it works as expected.

cp1 = ContourPlot[if1[x, y], {x, y} \[Element] em1, Mesh -> None, 
  PlotPoints -> 75, MaxRecursion -> 3, ContourShading -> None, 
  ContourStyle -> Red, Contours -> Range[0.05, 1, 0.1]]

I know how to extract the contours and transform them back to my original surface, but I have no idea how to plot them directly on the surface. SliceContourPlot3D should be able to plot on a region, but I haven't managed to get that to work when function values are defined on the surface only.

Now, my question: Is there an easier way to generate this mesh, ideally with more control over the mesh quality and avoid conversion from BoundaryMeshRegion? How to plot my contours directly on the original surface?

Any insights will be greatly appreciated.

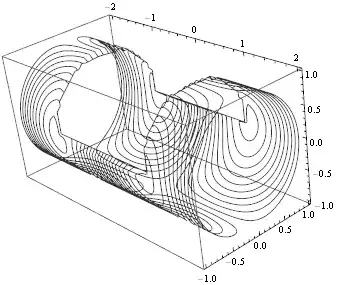
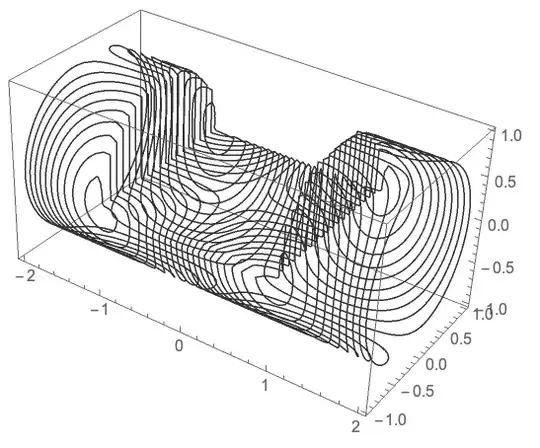
This probably isn't what you want, too simple, but what about just using the surface as the region for SliceDensityPlot3D, like SliceContourPlot3D[Sin[z Pi] Sin[u Pi], DiscretizeRegion@reg, {x, 0, 1}, {u, 0, 1}, {z, 0, 1}] - nevermind, for that your function needs to be defined at all points in 3D space — Jason B., Apr 13 '16 at 15:38
If you have the chance to upgrade to V10.4 things with ToBoundaryMesh will look much better. — user21, Apr 14 '16 at 02:18
@JasonB That's exactly what I tried to say. If my function is defined at least in some volume around the surface SliceContourPlot3D will work. But all I have is function values on the surface. — AxelF, Apr 14 '16 at 06:03
@AxelF - Is there any way to see the functional form for the current density? My electrodymanics is a bit shaky, but am I reading correctly that the surface density at any point on the surface would the product of some scalar field (depending on three spatial coordinates or on two coordinates defined within the surface only?) multiplied by the curl of the surface normal at that point on the surface (a vector quantity?). Sorry — Jason B., Apr 14 '16 at 07:22
@JasonB - You are right, the surface current density can be written as the curl of the normal vector multiplied by some scalar field, often called stream function, on the surface. I am working on an inverse problem: I know the desired magentic field and try to find an optimal current density, or finally a wire pattern, to generate this field. In my question, I've simplified this to Sin[z Pi] Sin[u Pi] since finding function values on the nodes is not the problem, it is about generating the mesh and plotting the function right on the surface in 3D. — AxelF, Apr 15 '16 at 06:07
@AxelF, so what are the coordinates there, the z and u? Are they cartesian spatial coordinates or are they some linear coordinates defined within the curved surface? I guess I feel like there has to be a better way to plot a function on a surface than evaluating the function at mesh points and then doing an interpolation function - mainly I say this because of the quality of the contour plot. Is there some reason why this is the preferred method? — Jason B., Apr 15 '16 at 06:58

score 10 · Answer 1 · answered Apr 18 '16 at 13:55

I haven't done the upgrade to 10.4, this is still stuck in our IT department...

Nevertheless, playing with different combinations of ToElementMesh, MeshRegion and RegionBoundary, I've come up with some reasonable results:

For my still rather simple example I use a cylinder with a cut-out.

reg1=Cylinder[{{-2,0,0},{2,0,0}},1];
reg2=Hexahedron[{{-1,-1,0},{-1,1,0},{1,1,0},{1,-1,0},{-1,-1,1},{-1,1,1}, {1,1,1},{1,-1,1}}];
reg=RegionDifference[reg1,reg2];
bdr=BoundaryDiscretizeRegion[reg,Method->Automatic,MaxCellMeasure->{"Length"->0.1}];
Show[bdr,Axes->True,AxesLabel->{"X","Y","Z"},Boxed->True]

As @user21 mentioned, ToBoundaryMeshin V10.4 will be even better, but this is good enough for now. Next step is to generate some dummy values on the mesh:

em=ToElementMesh[bdr,"MeshOrder"->1];
coordinates=em["Coordinates"];
dummy=Quiet[coordinates/.{x_Real,y_Real,z_Real}:>Sqrt[z^2+y^2]Cos[ArcTan[y,z]]Sin[x \[Pi]/2]/.Indeterminate->0.];
if=ElementMeshInterpolation[{em},dummy,"ExtrapolationHandler"->{Function[Indeterminate],"WarningMessage"->False}];

Now, if I plot this InterpolatingFunction over the surface defined with BoundaryDiscretizeRegion, the cut-out surfaces are missing.

But if I transfrom the ElementMesh to a MeshRegion and extract the boundary with RegionBoundary, I get what I expected:

mr=MeshRegion[em];
br=RegionBoundary[mr];
SliceContourPlot3D[if[x,y,z],br,{x,y,z}\[Element]mr,ContourShading->None,Contours->Range[-1.05,1.05,0.1],BoxRatios->{2,1,1}]

score 6 · Answer 2 · answered Mar 20 '20 at 12:53

Here is a way to get an improved boundary, for this you will need version 12.1 and make use of the new OpenCascadeLink:

Needs["OpenCascadeLink`"]
Needs["NDSolve`FEM`"]
reg1 = Cylinder[{{-2, 0, 0}, {2, 0, 0}}, 1];
reg2 = Cuboid[{-1, -1, 0}, {1, 1, 1}];
reg = RegionDifference[reg1, reg2];
ocr = OpenCascadeShapeBooleanRegion[reg];
bmeshOC = OpenCascadeShapeSurfaceMeshToBoundaryMesh[ocr];
bmeshOC["Wireframe"[
  "MeshElementStyle" -> Directive[FaceForm[Green], EdgeForm[Red]]]]

And then go ahead with:

em = ToElementMesh[bmeshOC, "MeshOrder" -> 1];
coordinates = em["Coordinates"];
dummy = Quiet[
   coordinates /. {x_Real, y_Real, z_Real} :> 
      Sqrt[z^2 + y^2] Cos[ArcTan[y, z]] Sin[x \[Pi]/2] /. 
    Indeterminate -> 0.];
if = ElementMeshInterpolation[{em}, dummy, 
   "ExtrapolationHandler" -> {Function[Indeterminate], 
     "WarningMessage" -> False}];
mr = MeshRegion[em];
SliceContourPlot3D[
 Sqrt[z^2 + y^2] Cos[ArcTan[y, z]] Sin[x \[Pi]/2], mr, 
 Element[{x, y, z}, mr], ContourShading -> None, 
 Contours -> Range[-1.05, 1.05, 0.1], BoxRatios -> {2, 1, 1}, 
 Boxed -> False, Axes -> None]

score 4 · Answer 3 · answered Apr 18 '16 at 14:11

4

It seems to me you can get the same result without invoking external packages or using an interpolation function, since you have a surface and you have a function defined at all points in space,

Taking your region bdr,

SliceContourPlot3D[
 Sqrt[z^2 + y^2] Cos[ArcTan[y, z]] Sin[x π/2], bdr, {x, -2, 
  2}, {y, -1, 1}, {z, -1, 1}, ContourShading -> None, 
 Contours -> Range[-1.05, 1.05, 0.1], BoxRatios -> {2, 1, 1}]

gives

answered Apr 18 '16 at 14:11

Jason B.

68,381
3
139
286

You are right, if I have a function fully defined in space, my approach is too complicated. But from my optimization, I will know my function values only on points on the surface. – AxelF Apr 21 '16 at 14:15
@AxelF - did you ever look at using ListSliceContourPlot3D? – Jason B. Mar 21 '17 at 16:55
I understand that this also requires the data to be given in a volume, nut just on a surface. – AxelF Mar 22 '17 at 07:47
@AxelF - I don't know how well it would work for a non-convex surface like this, but you can specify the points as a list of the form {{x, y, z f[x,y,z]}..} and those points don't need to form a rectangular grid. – Jason B. Mar 22 '17 at 10:59
I've tried to find an example: First a simple function on a grid: dataFull=Flatten[Table[{x,y,z,Sqrt[x^2+y^2+z^2]},{x,0,3,0.1},{y,0.0,3.0,0.1},{z,0.0,3.0,0.1}],2]; which I can plot on an implicitly defind plane: ListSliceContourPlot3D[dataFull,ImplicitRegion[z-y==0.1,{x,y,z}]]. Now, if I define my data on this plane only, it fails: With[{z=0.1},dataPlane=Flatten[Table[{x,y,y+z,Sqrt[x^2+y^2+z^2]},{x,0.0,3.0,0.1},{y,0.0,3.0,0.1}],1]];, ListSliceContourPlot3D[dataPlane,ImplicitRegion[z-y==0.1,{x,y,z}]] returns an empty plot. – AxelF Mar 22 '17 at 12:34

How to create a surface mesh embedded in 3D?

3 Answers3

Linked