Solving equation

Question

How can I solve this equation:

((a^2 - 1)*((a^2 - 1)*ArcTanh[a] - a))/(2*Sqrt[2*(a^2 - 1)^4]) == C*x

I am looking a solution for $a$ in function of $x$. I tried Solve and similar methods but I got unevaluated expression.

Answer 1

If it may also be a graphic solution? Consider:

FunctionDomain[ArcTanh[a], a]
(* -1 < a < 1 *)


((a^2 - 1)*((a^2 - 1)*ArcTanh[a] - a))/(2*Sqrt[2*(a^2 - 1)^4]) == c*x;
x[a_] = 1/c*((a^2 - 1)*((a^2 - 1)*ArcTanh[a] - a))/(2*Sqrt[2*(a^2 - 1)^4]);

With c as parameter

p = Plot[x[a] /. c -> 1, {a, -1, 1}, AxesLabel -> Automatic, GridLines -> Automatic]

p1 = Join @@ Cases[Normal@p, Line[x1__] :> x1, Infinity];
a = Interpolation@Thread@{Last /@ p1, First /@ p1}

Plot[a[x], {x, -3, 3}, GridLines -> Automatic, AxesLabel -> Automatic]

Edit

The easiest way to find the function a(x) is to build the inverse of f(a).

f = 1/c*((#^2 - 1)*((#^2 - 1)*ArcTanh[#] - #))/(2*Sqrt[2*(#^2 - 1)^4]) &;
a = InverseFunction@f

This function can be evaluated numerically with c as parameter, e.g.

c = 1;
Table[a[x], {x, -2, 2}] // N
(* {-0.888998, -0.76291, 0., 0.76291, 0.888998} *)

Plot[{f[x], a[x]}, {x, -2, 2}, GridLines -> Automatic, 
 PlotLegends -> {"f[x]", "a[x]"}, AspectRatio -> 0.8]

Edit 2

Please forgive me, I have a problem with the solutions. I follow here Michel E2's method.

f = ((a^2 - 1)*((a^2 - 1)*ArcTanh[a] - a))/(2*Sqrt[2*(a^2 - 1)^4]) - c x /. a -> a[x];
df = D[f, x] // Simplify

sol = DSolve[df == 0, a, x] /. C[1] -> 0

c = 1;
Plot[a[x] /. sol, {x, -2, 2}, GridLines -> Automatic]

Answer 2

I am going to give a generic answer which work in such cases. The main idea is to go numerical. You solve it for some parameter values and get an idea of the function which might be the answer.

dat = Table[{c, x, 
           a /. NSolve[((a^2 - 1)*((a^2 - 1)*ArcTanh[a] - a)) /(2*Sqrt[2*(a^2 - 1)^4])
       == c x && 0 < a < 10, a][[1]]}, {c, 0.1, 1, .1}, {x, 0.1, 1., .1}]

dat1 = Flatten[dat, 1];
f = Interpolation[dat1];
Plot3D[f[c, x], {c, 0.1, 1}, {x, 0.1, 1}]

Ignore the Solve::rantz error message. Note that I use [[1]] and a range 0 < a < 10. This comes handy if you have multiple root and also gives faster result because it looks for root only within that region.

Answer 3

One way: Derive the differential equation of the family (solve for the constant and differentiate); and use DSolve to solve it.

D[(1/x)((a^2 - 1)*((a^2 - 1)*ArcTanh[a] - a)) /
     (2*Sqrt[2*(a^2 - 1)^4]) /. a -> a[x], x] // Together // Numerator;
{dsol} = DSolve[% == 0, a, x] /. C[1] -> c
(*
  {{a -> Function[{x}, 
      InverseFunction[-(1/2) Log[1 - #1^2] + 
          1/2 Log[-ArcTanh[#1] - #1 + ArcTanh[#1] #1^2] &][c + Log[x]/2]]}}
*)

Evaluating an InverseFunction on exact input can sometimes take a long time. Be sure to use approximate machine reals when plotting or doing other numerical work. (This is accomplished by N below. Alternatively one could use the iterator {x, -1., 1.} instead of {x, -1, 1} to specify the plot domain.)

Block[{c = 1},
 Plot[a[N@x] /. dsol, {x, -1, 1}]
 ]

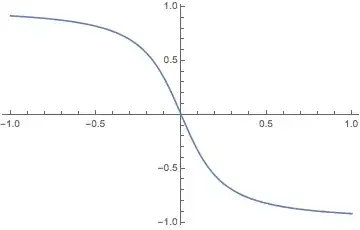
While InverseFunction can be inconvenient at times, the solution dsol does present a as a function of x and the parameter c.

---

Update: I guess I should point out that the inverse function is basically just the solution to the equation written in the form of an inverse function.

This simpler solution is equivalent to the produced by dsol:

{a -> Function[{x}, 
   InverseFunction[1/(1 - #1^2)*(-ArcTanh[#1] - #1 + ArcTanh[#1] #1^2) &][Exp[2 c] x]]}

It is equivalent to the OP's original equation via Exp[2 c] == 2 Sqrt[2] C. (Please note that capital C is a Protected Mathematica symbol.)