eigenoscillations of a sphere

Question

I would like to animate the eigenoscillations of a sphere (Earth?). It's just simple to draw images one by one:

SphericalPlot3D[{1 + 
   0.25*Re[SphericalHarmonicY[6, 3, th, phi]]}, {th, 0, Pi}, {phi, 0, 
  2 Pi}, PlotPoints -> {16, 32}]

but how to change m and l arbitrary to see, how a sphere vibrate. I've made this years ago, but I forgot.. Regards, Darko

Do you have an equation for how m and l change with time, or is it stochastic? (you say "arbitrary") — Jason B., Apr 20 '16 at 08:13
I would guess that (for the right set of equations) the dependence on t would be on the radial component. So simply varying the "amplitude" harmonically would yield a vibrating sphere. But what are the equations? Is it an elastic body? Is it an elastic body oscillating under its own gravity? Is it a bubble? These are different physical problems that would have different solutions. — gpap, Apr 20 '16 at 09:40

score 9 · Answer 1 · edited Apr 13 '17 at 12:55

9

So I can't seem to find a nice plottable form for the normal modes of an elastic sphere, if you can please let me know. This talks about the vector spherical harmonics, and people often show sketches of the displacements involved in the fundamental and overtones for the spheroidal and toroidal modes, but I don't find plottable equation forms for them (or I don't understand them enough to plot them).

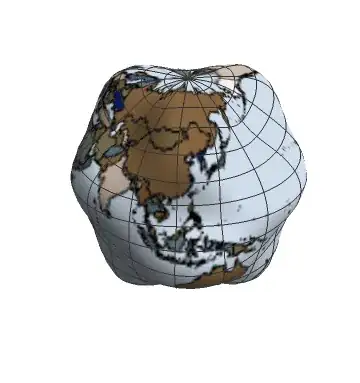
So let's just take your vibrational mode to be a simple cosine multiplying the spherical harmonic, and since we aren't actually modeling seismic activity we can just put a map of the Earth on the sphere to make it seem as though we are.

pic = Graphics[{EdgeForm[Black], 
   Table[{ColorData["DarkTerrain"][Random[]], 
     CountryData[
      country, {"FullPolygon", "Equirectangular"}]}, {country, 
     Append[CountryData[], "Antarctica"]}]}, 
  Background -> Lighter[ColorData["Aquamarine"][1], 0.5], 
  PlotRangePadding -> None];
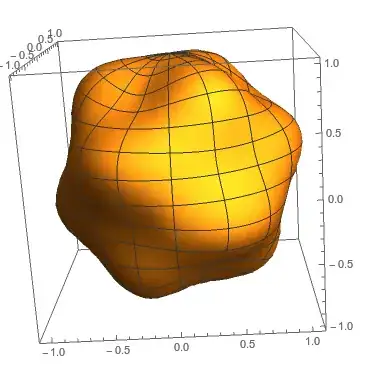
ListAnimate[SphericalPlot3D[1 + 0.25*Re[
        Exp[I 2 π #] SphericalHarmonicY[6, 3, u, v]], {u, 0, 
      Pi}, {v, 0, 2 Pi},
     PlotPoints -> 50,
     Mesh -> True,
     Axes -> False,
     TextureCoordinateFunction -> ({#5, 1 - #4} &),
     PlotStyle -> Directive[Texture[pic],
       Specularity[White, 50]], Lighting -> "Neutral",
     Boxed -> False] & /@ Range[0, 1, .01]];

edited Apr 13 '17 at 12:55

Community

1

answered Apr 20 '16 at 12:50

Jason B.

68,381
3
139
286

That's cool! +1 – Alexey Popkov Apr 20 '16 at 14:05
Thanks! I really wish I could actually plot the "normal modes of the earth", but this will suffice – Jason B. Apr 20 '16 at 14:10
Thank you, JasonB, it's just so, like a bubble of water in space. Only without Earth (no memory error). – Darko Apr 20 '16 at 14:11
@Darko - try removing the , TextureCoordinateFunction -> ({#5, 1 - #4} &), PlotStyle -> Directive[Texture[pic], Specularity[White, 50]], Lighting -> "Neutral" commands and add ColorFunction->(ColorData["TemperatureMap"][#6]&) – Jason B. Apr 20 '16 at 14:13
If that fails, take out the PlotPoints -> 50, – Jason B. Apr 20 '16 at 14:14
Almost got dizzy by looking at the solution. Imagine what would happen to inhabitants ... – yarchik Apr 20 '16 at 14:16

eigenoscillations of a sphere

1 Answers1