Finding very weak peaks

Question

I measured 1d particle oscillations. The particle is oscillating with a certain frequency, whereby its motion is disturbed.

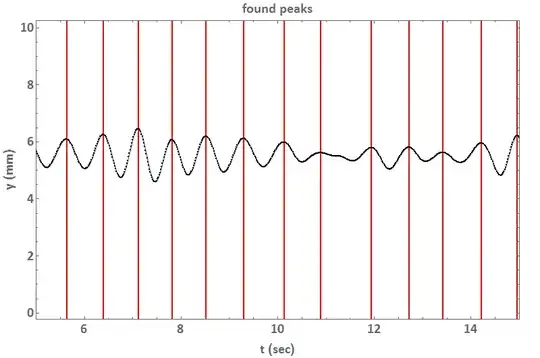
Now I would like to to find all peaks of the particles trajectory. One peak is nearly invisible and is not detected.

Here is my code:

data=<<"http://pastebin.com/raw/a4VUYAe3";

peaks=FindPeaks[data[[All,2]],0,0,-Infinity];
peaktimes=data[[Floor[First/@peaks],1]];
plot=ListLinePlot[data,PlotRange->{{5,15},All},Epilog->{PointSize[0.002],
      Point[data]},PlotRange->All,GridLines->{peaktimes,None},
      GridLinesStyle->Directive[Red,Thick]];

Show[plot,Frame->True,FrameLabel->{{"y (mm)",""},{"t (sec)","found peaks"}},
 BaseStyle->{FontWeight->"Bold",FontSize->20,
 FontFamily->"Calibri"},ImageSize->800]

The result is:

Is it possible to find also the very weak peak around t=11.3 sec?

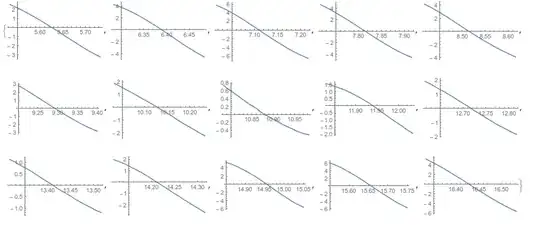
It's a shoulder, not a peak: ListLinePlot[data, PlotRange -> {{11.1, 11.4}, {5.46, 5.52}}, Mesh -> All, GridLines -> {None, {5.501}}]. — Alexey Popkov, Apr 20 '16 at 14:02
Just a philosophical question, imagine you find what you call the "weak peak", will it help you ? I mean, will it help you to solve the original problem? — yarchik, Apr 20 '16 at 14:07

score 9 · Answer 1 · answered Apr 20 '16 at 11:30

9

One way to define a peak is a point in the data where the derivative changes from positive to negative. Look at the behavior of the derivative near all the peaks you actually found,

df[xx_] = D[Interpolation[data][y], y] /. y -> xx;
Plot[df[xx], {xx, # - .1, # + .1}] & /@ peaktimes[[8 ;; 22]]

Now look at the shoulder at 11.3,

Plot[f[xx], {xx, 11.1, 11.4}]
Plot[df[xx], {xx, 11.1, 11.4}]

It isn't a peak therefore, there is no region of positive slope preceding the point where the slope approaches zero.

answered Apr 20 '16 at 11:30

Jason B.

68,381
3
139
286

Thank you for your answer ... the second derivative gives a minimum at about 11.31 where the expected peak should be. – mrz Apr 20 '16 at 13:15
Right on, but you can't go searching for all the minima in the second derivative, as that will give the inflection points between the peaks and valleys, right? – Jason B. Apr 20 '16 at 13:16
Yes. It would be a workaround to find this special "missing" peak ... – mrz Apr 20 '16 at 13:18

score 7 · Accepted Answer · edited Apr 13 '17 at 12:55

Is it possible to find also the very weak peak around t=11.3 sec?

It seems that the answer is yes, using my improvement/extension of Leonid Shifrin's approach for the question "Finding Local Minima / Maxima in Noisy Data".

This solution is not completely automated, it has some parameter tweaking, but I hope it is good enough.

Load the package:

Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/Applications/QuantileRegressionForLocalExtrema.m"]

After three-four experiments with picking different number of B-spline basis functions and a time interval, this code showed the weak peak:

Block[{data = data[[500 ;; 1000]], qfuncs},
 {qfuncs, extrema} = QRFindExtrema[data, 50, 2, 10, {0.99}];
 Show[{Plot[
    Through[qfuncs[x]], {x, Min[data[[All, 1]]], Max[data[[All, 1]]]},
     PlotStyle -> {Orange}, PerformanceGoal -> "Speed", Axes -> False,
     GridLines -> Automatic], 
   ListPlot[Join[{data}, extrema], 
    PlotStyle -> {{}, {PointSize[Medium], Red}, {PointSize[Medium], 
       Green}}]}, Frame -> True, PlotRange -> All]
 ]

Here are the extrema close to the mentioned time point:

Cases[extrema, {x_, _} /; 11 <= x <= 11.5, Infinity]

(* {{11.2333, 5.50068}, {11.1, 5.52349}} *)

Note, that I have taken a smaller time interval that contains the weak peak of interest. As I mentioned earlier, that manual tweaking might not desirable.

Finding very weak peaks

2 Answers2

Linked