Getting ordered coordinates out of ConvexHullRegion

Question

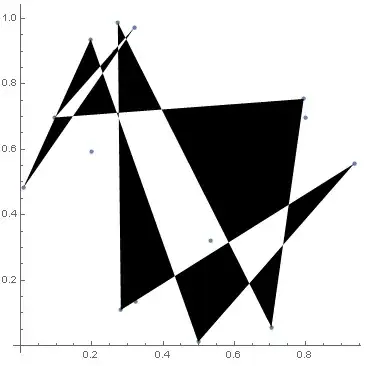
I'm trying to get the ordered coordinates of a convex hull using MeshCoordnates[ConvexHullMesh[data]], but the coordinates are uselessly out of order:

With[{d = RandomReal[{0, 1}, {20, 2}]},
 ListPlot[
  d,
  AspectRatio -> 1,
  Epilog -> Polygon[MeshCoordinates[ConvexHullMesh[d]]]
  ]
 ]

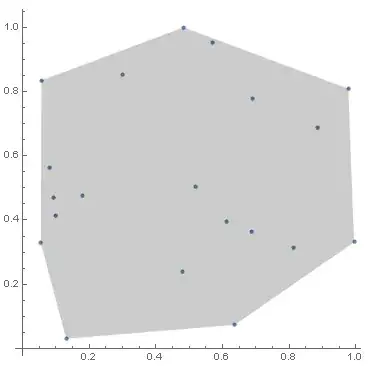
The older ComputationalGeometry`ConvexHull function works correctly:

Needs["ComputationalGeometry`"]
With[{d = RandomReal[{0, 1}, {20, 2}]},
 ListPlot[
  d,
  AspectRatio -> 1,
  Epilog -> {Opacity[0.2], Polygon[d[[ConvexHull[d]]]]}
  ]
 ]

Is there some way to get the ordered coordinates from ConvexHullMesh?

Edit: I need to manipulate the polygon; the goal is not to just display the graphics.

kglr · Accepted Answer · 2016-04-22T00:38:17.793

9

For graphing, my preferred approach is posted already by user21.

To get the ordered coordinates you can reorder MeshCoordinates[ConvexHullMesh[d] using FindCurvePath:

With[{d = RandomReal[{0, 1}, {20, 2}]}, mc=MeshCoordinates[ConvexHullMesh[d]];
ListPlot[ d, AspectRatio -> 1, Prolog -> {Yellow,Polygon[mc[[FindCurvePath[mc][[1]]]]]}]]

Mathematica graphics

An alternative way to get the ordering of the coordinates is to use the "BoundaryVertices" property of ConvexHullMesh[d]:

ConvexHullMesh[d]["BoundaryVertices"]

{1,8,4,5,6,3,10,9,2,7,11,1}

which is a rotated version of

FindCurvePath[MeshCoordinates[ConvexHullMesh[d]]][[1]]

{4,5,6,3,10,9,2,7,11,1,8,4}

And, the property "Coordinates" can be used instead of MeshCoordinates; so

#["Coordinates"][[#["BoundaryVertices"][[1]]]]&@ConvexHullMesh[d]

gives the ordered coordinates.

d = RandomReal[{0, 1}, {20, 2}];
chcoords=#["Coordinates"][[#["BoundaryVertices"][[1]]]]&@ConvexHullMesh[d];
ListPlot[ d, AspectRatio -> 1, Prolog -> {Yellow,Polygon[chcoords]}]

Mathematica graphics

Yet another way to get the ordered coordinates is to get the "GraphicsComplex" property and extract

Cases[Normal@ConvexHullMesh[d]["GraphicsComplex"],Polygon[x_]:>x,Infinity][[1]]

edited Apr 22 '16 at 00:38

answered Apr 21 '16 at 23:07

kglr

394,356
18
477
896

Thanks, didn't know about FindCurvePath. I wonder if the ComputationalGeometryPackage uses that internally, or if it has a more direct and efficient approach (assuming FindCurvePath is somewhat expensive?). – ZachB Apr 21 '16 at 23:15
@ZachB, Thank you for the accept. I am not familiar with the ComputationalGeometry package, but we should be able to see the code for ConvexHull function. – kglr Apr 21 '16 at 23:19
1

@ZachB, you can see the code for ConvexHull using nb = NotebookOpen[ ToFileName[{$InstallationDirectory, "AddOns", "Packages", "ComputationalGeometry"}, "ComputationalGeometry.m"]]; NotebookFind[nb, "compute 2D convex hull using Graham's scan \ algorithm"] – kglr Apr 21 '16 at 23:26
When I copy you code I find a some parenthesis out of sync also added a more efficient way then FindPath – user21 Apr 21 '16 at 23:41
@user21, thank you; i added the missing {. – kglr Apr 21 '16 at 23:56
1

Hi, kglr. ConvexHullMesh does not have properties like "BoundaryVertices" at least in 13.2. So this answer needs an update. – matheorem Jul 09 '23 at 10:02

user21 · Answer 2 · 2016-04-21T23:38:49.613

8

Assuming the goal is to create the graphics:

With[{d = RandomReal[{0, 1}, {20, 2}]},
 Show[ListPlot[d, AspectRatio -> 1], ConvexHullMesh[d]]]

And here is a more efficient version than FindPath:

With[{d = RandomReal[{0, 1}, {20, 2}]}, 
 ListPlot[d, AspectRatio -> 1, 
  Epilog -> 
     GraphicsComplex[
      MeshCoordinates[#], {Opacity[0.2], MeshCells[#, {2, All}]}] &[
   ConvexHullMesh[d]]]]

edited Apr 21 '16 at 23:38

answered Apr 21 '16 at 23:00

user21

39,710
8
110
167

Sorry, just clarified in question -- I actually need the points that comprise the polygon so I can manipulate the hull, so the goal is not (immediately) to create the graphics. – ZachB Apr 21 '16 at 23:12
@ZachB, added a more efficient version. – user21 Apr 21 '16 at 23:39
1

Thanks, wish I could select multiple answers. +1'ed. – ZachB Apr 22 '16 at 00:14
1

@ZachB, no worries, I am no a hunter-gatherer any longer ;-) – user21 Apr 22 '16 at 00:27

score 7 · Answer 3 · 2016-04-22T15:09:02.640

7

d = RandomReal[{0, 1}, {20, 2}];
hull = ConvexHullMesh[d];

The ordering can be obtained directly using MeshCells:

MeshCells[hull, 2]
(* {Polygon[{2, 6, 5, 4, 3, 1}]} *)

So:

points = MeshCoordinates[hull];
order = MeshCells[hull, 2][[1, 1]];
Graphics[{Yellow, Polygon[points[[order]]], Black, Point[d]}]

edited Apr 22 '16 at 15:09

answered Apr 21 '16 at 23:40

Another good answer, thanks! – ZachB Apr 22 '16 at 00:13

score 6 · Answer 4 · answered Apr 22 '16 at 12:03

pts = RandomReal[1, {20, 2}];
mesh = ConvexHullMesh[pts]

You can simple use MeshPrimitives.

MeshPrimitives[mesh, 2]
(* {Polygon[{{0.135494, 0.556868}, {0.147549, 0.121726}, 
             {0.423421, 0.0565637}, {0.894244, 0.172512}, 
             {0.917483, 0.413526}, {0.911708, 0.8986}, 
             {0.708881, 0.866828}, {0.272797, 0.654125}}]} *)

A 2D convex hull mesh will consist of a single Polygon. Coordinates are easy to extract from there.

MeshCells does the same, but uses point indices instead of point coordinates.

score 2 · Answer 5 · edited Jul 10 '23 at 02:44

2

using ConvexHullRegion

d = RandomReal[{0, 1}, {20, 2}];
ConvexHullRegion[d]
First@ConvexHullRegion[d]

gives

edited Jul 10 '23 at 02:44

ZachB

1,200
9
19

answered Jul 09 '23 at 10:09

matheorem

17,132
8
45
115

Getting ordered coordinates out of ConvexHullRegion

5 Answers5