Multiply integrand with -1, and the precision changes?

Question

"After multiplying the integrand of NIntegrate with -1, the Precision of the output will change." ← Sounds silly, huh? But this seems to be true at least for numerical integral internally using "ExtrapolatingOscillatory" method. Just try the following example:

Precision /@ 
 NIntegrate[{1, -1} BesselJ[0, x], {x, 0, ∞}, WorkingPrecision -> 32, 
  Method -> "ExtrapolatingOscillatory"]

{31.0265, 25.0279}

It's not necessary to set Method -> "ExtrapolatingOscillatory" manually in this sample, I added the option just to emphasize.

Of course in the above example the difference of precision is small and isn't a big deal, but in some cases the difference can be drastic, for example the following I encountered in this problem:

f[p_, ξ_] = -(5 p Sqrt[(5 p^2)/6 + ξ^2] )/(
  4 (-4 ξ^2 Sqrt[(5 p^2)/6 + ξ^2] Sqrt[(5 p^2)/2 + ξ^2] + ((5 p^2)/2 + 2 ξ^2)^2));

pmhankel[p_, sign_: 1, prec_: 32] := 
 NIntegrate[sign ξ BesselJ[0, ξ] f[p, ξ], {ξ, 0, ∞}, 
  WorkingPrecision -> prec, Method -> "ExtrapolatingOscillatory"]

preclst = Table[Precision@pmhankel[#, sign] & /@ Range@32, {sign, {1, -1}}]

ListLinePlot[preclst, PlotRange -> All]

It's not necessary to set Method -> "ExtrapolatingOscillatory" manually in this sample, I added the option just to emphasize.

How to understand the behavior? Except for calculating every integral twice and choosing the better one, how to circumvent the problem?

No. Doesn't sound silly to me. (1) NIntegrate does some symbolic pre-processing and anything you do you might affect that. That is reason enough to not find this surprising. If you haven't already, try ("SymbolicProcessing"->0). (2) And are you absolutely sure that changing the sign wouldn't significantly affect the evaluation for the numerical method you chose? That isn't obvious to me either. (https://reference.wolfram.com/language/tutorial/NIntegrateIntegrationStrategies.html#50593814) — Searke, Apr 22 '16 at 15:14
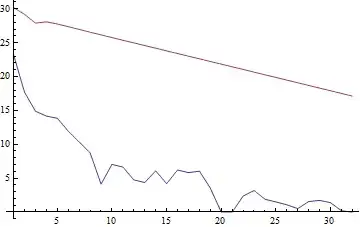
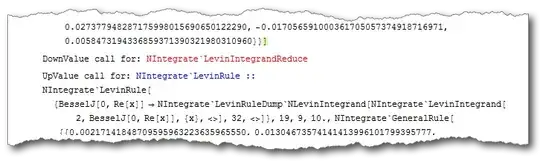
Yes, I wouldn't expect "ExtrapolatingOscillatory" to work without preliminary symbolic processing, how else can the zeroes where the integrand will be split at be determined? — J. M.'s missing motivation, Apr 23 '16 at 06:06
@Searke Thanks for the response. (1) With "SymbolicProcessing->0" the problem remains: pmhankelTest[p_, sign_: 1, prec_: 16] := NIntegrate[sign ξ BesselJ[0, ξ] f[p, ξ], {ξ, 0, ∞}, WorkingPrecision -> prec, Method -> {"ExtrapolatingOscillatory", "SymbolicProcessing" -> 0}];pmhankelTest[32, #, 32] & /@ {-1, 1} (2) I tried IntegrationMonitor mentioned in this answer, the {"Boundaries", "Dimension", "Error", "GetRule", "Integrand"} etc. seems to be all the same, and the only difference between "Integral" is the sign. — xzczd, Apr 23 '16 at 06:22
@J.M. I also tried manually implement "ExtrapolatingOscillatory", and the problem doesn't show up in my (much slower) implementation: zero[i_] := Piecewise[{{BesselJZero[0, i], i > 0}}];separatepmhankel[p_?NumericQ, sign : 1 | -1, i_?NumericQ, prec_] := NIntegrate[sign ξ BesselJ[0, ξ] f[p, ξ], {ξ, zero@i, zero[i + 1]}, WorkingPrecision -> prec, MaxRecursion -> 40]; manualpmhankel[p_, sign_: 1, prec_: 16] := NSum[separatepmhankel[p, sign, i, prec], {i, 0, Infinity}, Method -> "AlternatingSigns", WorkingPrecision -> prec]; manualpmhankel[32, #, 32]&/@{1,-1} // AbsoluteTiming — xzczd, Apr 23 '16 at 06:27
@xzczd Changing BesselJ[0, x] to BesselJ[0, Re[x]] solves the issue. — , Apr 23 '16 at 12:30
@Xavier Interesting. Using the code in the update of this answer, I found that in this case NIntegrate internally switches to "LevinRule", and the output is indeed the same as that with option , Method -> "LevinRule". How about giving an answer? — xzczd, Apr 25 '16 at 05:54
@xzczd I was not sure why replacing x by Re[x] in your expression made it work, although I supposed this was related to some internal symbolic checks. The post you linked is interesting and your analysis provides the answer. Please feel free to answer your post, you've done all the work. — , Apr 26 '16 at 18:25

score 7 · Answer 1 · edited Apr 13 '17 at 12:55

Short answer:

One workaround is to use Method -> "LevinRule" instead.

Long answer:

As mentioned by Xavier in a comment above, changing BesselJ[0, x] to BesselJ[0, Re[x]] resolves the issue:

NIntegrate[{1, -1} BesselJ[0, Re@x], {x, 0, ∞}, WorkingPrecision -> 32, 
 Method -> "ExtrapolatingOscillatory"]
    Precision /@ %

{0.99999999999999999999999999999979, -0.99999999999999999999999999999979}
{32., 32.}

But why it works? Codes in the UPDATE of this answer solve the mystery. The truth is, NIntegrate has internally switched to "LevinRule":

Pictured by Simon Wood's shadow.

The output is indeed the same as that with option Method -> "LevinRule:

NIntegrate[{1, -1} BesselJ[0, x], {x, 0, ∞}, WorkingPrecision -> 32, 
 Method -> "LevinRule"]
Precision /@ %

{0.99999999999999999999999999999979, -0.99999999999999999999999999999979}
{32., 32.}

Notice in this case you'll be unable to adjust the MaxRecursion option because of a bug mentioned here, but this seems not to be a big deal:

pmhankelLevin[p_, sign_: 1, prec_: 32] := 
 NIntegrate[sign ξ BesselJ[0, ξ] f[p, ξ], {ξ, 0, ∞}, 
  WorkingPrecision -> prec, Method -> "LevinRule"]

lst1 = pmhankel[#, -1] & /@ Range@32;
(* You'll see warning NIntegrate::ncvb and be unable to eliminate it 
   by adjusting MaxRecursion option because of the bug mentioned above 
   when generating lst2 and lst3 *)
lst2 = pmhankelLevin /@ Range@32;
lst3 = pmhankelLevin[#, -1] & /@ Range@32;
(* But the difference between lst2, lst3 and lst1 is negligible: *)
Max /@ {(lst1 + lst2)/lst1, (lst1 - lst3)/lst1}

{2.27320119973*10^-6, 2.27320119973*10^-6}

Though a workaround is found, the reason why the precision is influenced by the sign when "ExtrapolatingOscillatory" method is used still remains unclear. I'm looking forward to answer(s) addressing the issue.

ilian · Accepted Answer · 2016-08-08T20:15:39.527

The oddity in this case comes from NSum which is being called in a certain way from NIntegrate. This is a simple example that has roughly the same behavior (note in this case the exact result is known to be $\mp \ln 2$):

NSum[(-1)^n/n, {n, 1, Infinity}, 
          Method -> {"AlternatingSigns", Method -> "WynnEpsilon"}, WorkingPrecision -> 32]

(* -0.6931471805599453094172318803247 *)

NSum[-(-1)^n/n, {n, 1, Infinity}, 
          Method -> {"AlternatingSigns", Method -> "WynnEpsilon"}, WorkingPrecision -> 32]

(* 0.693147180559945309417232 *)

where the second result has several digits fewer than the first.

Is that a bug? Not necessarily, because both results have at least 16 correct digits which certainly attains the default PrecisionGoal, which is WorkingPrecision/2.

Still, I agree the consistency could be improved in this case and I have filed a report for the developers to take a look.

Update

This has been improved in the just released Mathematica 11.0.

Multiply integrand with -1, and the precision changes?

2 Answers2

Linked