Delaunay Triangulation for 3D Surface Data

Question

I want to do a Delaunay triangulation on scattered 3D surface data. Mathematica itself does it only for 2D through the command DelaunayTriangulation[], which gives a triangulation for points in a plane. I also tried the MathLink package "TetGenLink", which can itself perform a Delaunay triangulation for three-dimensional data. The problem here is that TetGenDelaunay[] produces a triangulation through the inner region of the data, but I can't see how I can manage that the triangulation is only done for the surface (like what is done by MATLAB's DelaunayTri (see this SO question).

So, performing a Tetrahedralization and keeping only the surface triangles isn't a valid solution — Dr. belisarius, Oct 01 '12 at 12:22
Access to some possibly relevant internal routines may be found at Demonstrations here and here. This one might also be useful. — Daniel Lichtblau, Dec 04 '12 at 15:06
@Daniel The last one doesn't work with Mathematica 9. (It does with Mathematica 8.) — Szabolcs, Dec 13 '12 at 15:43
@Daniel & anyone else who might try the demonstration: It seems that the breakage is because of a change from a 0-based indexing to 1-based indexing in the tetgen library (not high level Mathematica) function getFaces. It can be corrected by removing the +1 from getFacesFun@outInst in the ch function in the demonstration source code. — Szabolcs, Dec 13 '12 at 16:05

RunnyKine · Answer 1 · 2014-08-12T03:32:27.440

10

In Version 10, this can be done elegantly in one line:

SeedRandom[400]
pts = RandomReal[5, {400, 3}];

Then:

surftri = RegionBoundary @ TriangulateMesh @ DelaunayMesh @ pts

Mathematica graphics

We can look inside to see that only the surface triangulation remains:

HighlightMesh[surftri, {Style[0, Directive[PointSize[0.015], Blue]], Style[1, Thin, Black], 
  Style[2, Opacity[0.7], Cyan]}]

Mathematica graphics

edited Aug 12 '14 at 03:32

answered Aug 12 '14 at 02:51

RunnyKine

33,088
3
109
176

score 9 · Answer 2 · 2012-12-13T08:03:40.640

9

As you state, TetGenDelaunay is for a tetrahedralization of the 3D space of the input data, and you'd then need to extract the surface triangulation. So for TetGenDelaunay there is no way around the tetrahedralization. (But I wonder if this is not also the case for DelaunayTri) TetGen is quite efficient, so maybe this is still an option. Perhaps, depending on the purpose of your computation, you could make use of ListSurfacePlot or RegionPlot3D.

In any case, here is how you'd extract the surface from the tetrahedralization:

Needs["TetGenLink`"]
data3D = RandomReal[{0, 1}, {1000, 3}];
in = TetGenCreate[];
TetGenSetPoints[in, data3D];
out = TetGenTetrahedralize[in, ""];
coords = TetGenGetPoints[out];
(* issue in TetGen interface, thus + 1 *)
surface = TetGenGetFaces[out] + If[$VersionNumber < 9.0, 1, 0];
Graphics3D[GraphicsComplex[coords, Polygon[surface]], Boxed -> False]

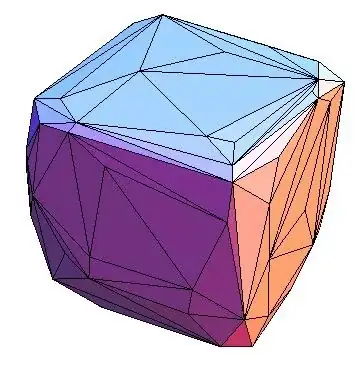
surface tetrahedalization

To set vertex colors you can use:

values = Sqrt[Total[coords^2, {2}]];
cf = ColorData["TemperatureMap"];
vc = Developer`ToPackedArray@(List @@@ (cf[#] & /@ values));
Graphics3D[{Opacity[0.5],
 GraphicsComplex[coords, Polygon[surface], VertexColors -> vc]}, 
 Boxed -> False]

surface tetrahedalization, with colors

edited Dec 13 '12 at 08:03

answered Oct 01 '12 at 12:25

@J.M. thanks for fixing my poor spelling! – Oct 01 '12 at 13:26
You're welcome! I initially considered using TetGen too, but I got bogged down in figuring how to pick out the outermost polygons. I didn't know it was this easy! – J. M.'s missing motivation Oct 01 '12 at 13:30
@J.M. do you think the documentation would benefit from such an example? – Oct 01 '12 at 13:31
Looking around, surface triangularization seems to be a quite common task, so yes, I think including such an example in the docs would be nice. – J. M.'s missing motivation Oct 01 '12 at 13:35
Hi, it's in SystemFiles/Links/TetGenLink – Dec 06 '12 at 04:06
@ruebenko in V9 this solution produces rather different output? – Yves Klett Dec 12 '12 at 15:45
@YvesKlett, thanks, fixed. – Dec 13 '12 at 08:03
Isn't the boundary of the Delaunay tetrahedralization just the convex hull of the data, which can be found in much more straightforward ways? – Aug 12 '14 at 07:49

Delaunay Triangulation for 3D Surface Data

2 Answers2