Issues with modeling pulses in a very simple system of DAEs

Question

Bug introduced in 10.4.1 or earlier and fixed in 11.0.0

Bug has been confirmed by WRI [Case:3594387]:

It does appear that the NDSolve function is not behaving properly in this case and an incident report has been created with the information you provided.

---

Some time ago I had asked this question about evaluation difficulties using Euler Integration to solve a system of ODE where discrete pulses occur.

While I have now abandoned Euler integration and can thus make use of DiracDelta to model pulses trying to introduce algebraic equations seems to pose a problem:

Modeling an account with deposits

Consisder the most simple problem in Economics and Business, e.g. modeling a bank account with interest:

• $x(t)$ is to designate the amount of money in the bank account; at the beginning there will be 100 units of money in the account ($x(0) = 100$)
• there will be interest paid at a fractional rate ot $r = 0.05$ per unit of time
• There will be a deposit of +10 units at times $t_1 = 3$ and $t_2 = 6$
• The account is to be simulated for 10 periods

Setting this up with NDSolve is rather straight forward and works fine:

deposit = Function[t, 
    Total @ {
        10. DiracDelta[ t - 3 ],
        10. DiracDelta[ t - 6 ]
    }
];

sim = First @ NDSolve[
    {
        x[0] == 100.,
        x'[t] == 0.05 x[t] + deposit[t]
    },
    x,
    { t, 0, 10 }
];

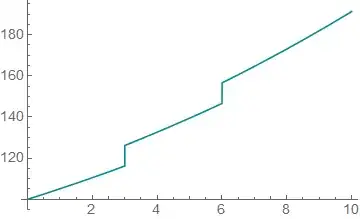
Plot[ Evaluate @ ( x[t] /. sim ), { t, 0, 10 }]

... but will not work as DAEs (with a simple output function)

But what if this is set up as a differential algebraic equations model and there is to be some kind of system output as the engineers do in their control system framework (cf. NonlinearStateSpaceModel)?

More precisely: What happens if there is some function of the stock $y(t) = g(x(t))$ or even more simple some function of time $y(t) = g(t)$?

simDAE = First @ NDSolve[
    {
        x[0] == 100.,
        x'[t] == 0.05 x[t] + deposit[t],

        y[0] == 1.,
        y[t] == 1. (* so our g() is simply a constant *)
    },
    {
        x, y
    },
    { t, 0, 10 }
];

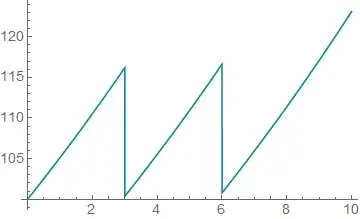
Plot[ Evaluate @ ( x[t] /. simDAE ), {t, 0, 10} ]

Surprisingly this simple system is not simulated correctly begging the question:

What is going on here? Why are the pulses evaluated with the wrong sign?

UPDATE

Using another Method as has been suggested by MichaelE2 below will work for the very simple case so far, but unfortunately not for the more general case, e.g.

simDAE2 = First @ NDSolve[
    {
        (* modeling the system *)
        x[0] == 100.,
        x'[t] == 0.05 x[t] + deposit[t],

        (* modeling the system's output *)
        y[0] == x[0],
        y[t] == x[t]
    },
    { x, y},
    { t, 0, 10 },
    Method -> { "EquationSimplification" -> "MassMatrix" }
];

Row @ Map[
    Plot[ Evaluate @ (#[t] /. simDAE2 ), 
          {t, 0, 10}, 
          ImageSize -> {GoldenRatio 200, 200}, 
          PlotLegends -> Placed[ ToString @ #, Below]] &,
    {x, y}
]

Answer 1

Below is a workaround for the simple case. The OP can say whether it works more general. I haven't quite tracked down yet why the system is set up incorrectly with the default Method -> {"EquationSimplification" -> "Solve"} and with Method -> {"EquationSimplification" -> "Residual"}. But it works in this case with Method -> {"EquationSimplification" -> "MassMatrix"}.

simDAE = First@
   NDSolve[{x[0] == 100., x'[t] == 0.05 x[t] + deposit[t], y[0] == 1.,
      y[t] == 1. }, {x, y}, {t, 0, 10},
    Method -> {"EquationSimplification" -> "MassMatrix"}];

Plot[Evaluate@(x[t] /. simDAE), {t, 0, 10}]

---

Update: Response to comment

Again, I can only present a potential workaround at this point. Constructing a WhenEvent[] seems to work better than the automatic processing of DiracDelta[] in this case. For what it's worth, here's a function to convert deposit to a sequence of events, but it's probably easier to use its last line to construct the sequence directly from the times and amounts.

ClearAll[diracToEvent];
diracToEvent[depositFn_, x_, t_, scale_: 1/2] :=
  Module[{
    times = 
     Union @@ Cases[depositFn, DiracDelta[e_] :> (t /. Solve[e == 0, t]), Infinity],
    dt,
    amounts},
   With[{xt = If[MatchQ[x, _[t]], x, x[t]]},
    dt = Min@Differences@times;
    amounts = Integrate[depositFn, {t, # - dt*scale, # + dt*scale}] & /@ times;
    MapThread[
     WhenEvent[t > #1, xt -> xt + #2] &,
     {times, amounts}
     ]
    ]
   ];

simDAE = First@NDSolve[{
     x[0] == 100., x'[t] == 0.05 x[t], y[t] == 25 Log[x[t]] ,
     diracToEvent[deposit[t], x, t]},
    {x, y}, {t, 0, 10}
    ];

Plot[Evaluate@({x[t], y[t]} /. simDAE), {t, 0, 10}]