Good way to create a similarity / distance matrix for a large dataset

Question

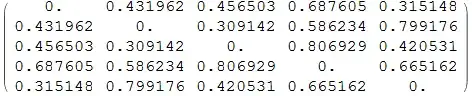
I have a large dataset with rows (100k+) for products and columns for features.

Now I want to create a similarity matrix with NormalizedSquaredEuclideanDistance. The desired output would be a symmetric matrix with products as columns and rows and the similarity measures as entries.

For[p = 1, p <= Length[dataset[[All,1]]], p++, 
  For[n = 1, n <= Length[dataset[[All,1]]], n++,
    SimMat[[p, n]] = 
      NormalizedSquaredEuclideanDistance[
        dataset[[n, 2 ;; Length[dataset[[n]]]]], 
        dataset[[p, 2 ;; Length[dataset[[p]]]]]]]

There are some problems:

NormalizedSquaredEuclideanDistance does not work with how I called the rows.
Using two For-loops for such a big dataset seems not very efficient,

I am finding it hard to understand this question. Can you give us a small example of input along with the output you expect from this example? By small, I mean an input matrix of dimension, say, 4 x 4. — m_goldberg, May 01 '16 at 12:51
Is your dataset / product-feature matrix sparse? For example, if you have 100 feature-columns, for a given product $p$ do all feature-columns have associating values with $p$? — Anton Antonov, May 01 '16 at 17:09
It is sparse, as many columns are dummies for categorical features. — Zappageck, May 03 '16 at 05:21

score 9 · Accepted Answer · answered May 01 '16 at 16:56

9

If you have Mathematica 10.3 or above you can use DistanceMatrix:

DistanceMatrix[dataset2, DistanceFunction -> NormalizedSquaredEuclideanDistance]

I'm assuming the same data as defined by kglr, you have not given us an example. If you don't have Mathematica 10.3 there's still HierarchicalClustering`DistanceMatrix which is used in the same way.

answered May 01 '16 at 16:56

RunnyKine

33,088
3
109
176

I up-voted this answer because of the use of DistanceMatrix, but DistanceMatrix can be much slower than Outer for a list of sparse vectors. – Anton Antonov May 01 '16 at 21:36
@AntonAntonov. Thanks. Do you know why that is the case? – RunnyKine May 01 '16 at 21:39
Sorry, no. I just did some benchmarking with Outer and DistanceMatrix. – Anton Antonov May 01 '16 at 22:59
@AntonAntonov but DistanceMatrix is orders of magnitude faster than Outer for normal matrices. – Sjoerd C. de Vries May 03 '16 at 06:25
@SjoerdC.deVries May be it is a good idea to have an answer with benchmarking. – Anton Antonov May 03 '16 at 10:02

score 5 · Answer 2 · answered May 01 '16 at 13:00

5

dataset2 = RandomReal[1, {5, 7}]; (* this stands for dataset[[All,2;;]] in your case*)

dataset2 // MatrixForm

Mathematica graphics

output = Outer[NormalizedSquaredEuclideanDistance, dataset2, dataset2, 1];
output // MatrixForm

Mathematica graphics

answered May 01 '16 at 13:00

kglr

394,356
18
477
896

Good way to create a similarity / distance matrix for a large dataset

2 Answers2